Verification of Class B S-N Curve for Fatigue Design of Steel Forgings
Yan-Hui Zhang and Stephen J Maddox
Integrity Management Group, TWI Ltd, Granta Park Great Abington, Cambridge, CB21 6AL, UK
Siakzar ManteghiF
UEC Mechanical & Materials Engineering Team, BP Exploration Operating Company Limited, Chertsey Road, Sunbury, TW16 7LN, UK
Paper published in International Journal of Fatigue 92 (2016) 246–261
Abstract
Currently the fatigue design procedure for forged steel connectors in steel catenary risers (SCRs) is based on the BS 7608 Class B S-N curve. However, there is very little direct support for this. Therefore, a fatigue testing programme, including strip specimens and small-scale cylindrical machined specimens extracted from actual forged J-lay connectors, was carried out to establish a suitable fatigue design procedure. The effects of stress ratio and surface roughness on fatigue strength were investigated. On the basis of these test results, together with available published data obtained from specimens that failed in plain steel, the Class B S-N curve was verified. The method was particularly conservative for low stress ratios in the high-cycle regime and a procedure based on the use of the Goodman diagram was devised for correcting the Class B curve for mean stress. Surface roughness in the range investigated, between 3.2 and 8.1μm in Ra, had little effect on the fatigue performance of the forged steel.
1. Introduction
Steel catenary risers (SCRs), made up of lengths of pipe girth-welded together with forged steel connectors introduced periodically to facilitate J-lay installation, provide a potential solution for deepwater oil and gas production. However, they are subject to severe fatigue loading. Some current projects involving the design of deepwater SCR systems have drawn attention to doubts surrounding the fatigue design procedure for plain steel components, such as forged steel mechanical connectors or J-lay collars. Although in general it is expected that the girth welds will govern allowable design stresses in the riser, the possibility that geometric stress concentrations in the forgings could result in lower fatigue lives cannot be discounted.
The fatigue design of forgings is commonly based on the BS 7608 Class B S-N curve (1). However, there is very little direct evidence, including from tests on actual forged components, to support this approach. In contrast, there is a substantial database obtained from structural components such as pressure vessels and pipes (2-4), which suggests that the Class B S-N curve may be too high, especially in the long-life regime that is of primary relevance to SCRs. As indicated in Figure 1, the lower Class C may be more suitable. An important feature that may invalidate this database is the surface finish of the components concerned, which varied from as-received plate to machined pressure vessels. The relatively smooth surface finish adopted for forged pipeline components may result in considerably better fatigue performance than the structural components featured in the database. However, this needs to be confirmed.
On the other hand, the fatigue performance of forged pipeline components may be better than Class B. Apart from the anticipated benefit of a good surface finish it should be borne in mind that Class B was derived on the basis of fatigue test results obtained from welded specimens (5). These were continuous longitudinal butt welds, which are the highest fatigue strength weld details, and fatigue cracking generally initiated on the surface from weld ripples. Thus, their surface finish is not at all comparable with that for machined components. In addition, the welded specimens used to generate the Class B data will certainly have contained very high tensile residual stresses. These have the effect of producing very high effective mean stresses regardless of the applied mean stress, resulting in fatigue performance that reflects the most severe applied tensile mean stress conditions. Such conditions would be too severe for many practical applications of plain steel components, making the Class B curve too conservative. Having said this, parts of a riser system operate under relatively high static stresses which result in high stress ratios (R = minimum/maximum applied stress), up to 0.8, when the fatigue loading is superimposed. Thus, high mean stress conditions are also relevant in this context. In general, it will be evident that fatigue design guidance is required for the full range of applied mean stresses.
In view of the situation described above, a testing programme was carried out to produce a relevant fatigue database and to establish a suitable fatigue design procedure for plain steel components, focusing particularly on large forged steel pipe connectors.
2. Approach
Two types of tests were carried out to evaluate the fatigue design of steel forgings. Both were based on fatigue endurance data obtained experimentally from the steel used for the mechanical connector. The first type of tests was performed on strip specimens extracted from actual forged J-lay connectors. These specimens retained the geometric details and the surface finish of the connector. Consequently, it was hoped that they would exhibit very similar fatigue performance to the full-scale connector and hence provide relevant fatigue data directly. This approach is similar to that widely used to evaluate girth welds. The influence on fatigue strength of surface finish and applied mean stress were investigated with these specimens.
The second type of tests was that commonly used in the fatigue design of machined components, using fatigue endurance data obtained from small-scale smooth specimens of the material. Fatigue curves based on such data are used in conjunction with an appropriate stress concentration factor (SCF) or fatigue strength reduction factor, for the geometry of the actual component, to calculate its fatigue life. To investigate this approach, fatigue tests were performed on small cylindrical specimens without stress concentration features. However, rather than using polished specimens, the specimens were prepared to the same surface finish as the mechanical connector after machining. This avoided the need to apply any correction factors other than the geometric SCF associated with the mechanical connector. Both low-cycle fatigue (LCF) tests under strain control and high-cycle fatigue (HCF) tests under load control were carried out to generate the relevant endurance database.
In addition, the published data obtained from specimens that failed in plain steel were also analysed to evaluate the fatigue design of steel forgings.
3. Experiments
3.1 Materials
Test specimens were taken from two forged steel pipe connectors with J-lay collars, Figure 2. The outside diameter (OD) and the wall thickness (WT) of the pipe away from the collar were 610.0mm and 26.7mm, respectively. The stress at the cross section with this smallest WT was defined as the nominal stress. This WT increased to ~32.5mm approximately 58mm from the collar. The OD and the length of the collar were 809.5mm and 153.7mm, respectively, giving a collar height of ~94mm above the adjacent pipe surface. The connectors were made of A707 steel with specified minimum yield (SMYS) and tensile (SMTS) strengths of 448MPa and 552MPa respectively.
3.2 Strip specimens
3.2.1 Specimen design and stress analysis
With the aim of designing strip test specimens that retained the features that were expected to influence fatigue strength, notably geometric details and surface finish, finite element (FE) modelling of the stress distribution was implemented using ABAQUS FE analysis software. Eight‑noded brick elements with reduced integration were used (ABAQUS element code C3D8R). The mesh was refined around the anticipated stress concentration regions, the thickness and width transitions on the outer surface. The model was elastic with a Young's Modulus of 207,000MPa and a Poisson's ratio of 0.3.
It was anticipated that waisted strip specimens with the collar in the middle, along the lines of that shown in Figure 3, would be suitable. A preliminary analysis of a full-scale model of a connector in tension indicated that the region with the highest SCF, defined as the local stress divided by the nominal stress, was the wall thickness transition radius, not the collar corner radius. The same was found by FEA of a strip specimen under axial loading, although the SCFs were lower in the strip than in the full-scale model (1.28 compared with 1.77). In this case, the model assumed that the clamps that gripped the specimen in the testing machine were stiff and, therefore, that it was fixed in all directions at the clamping surfaces. Appropriate boundary conditions were applied to simulate the half width symmetry. The strip specimen model was then modified to explore the effect of removing part of the collar, anticipating that this would reduce the difficulty and cost of producing specimens from the connector. This showed that there was no change in the SCF at the thickness transition radius, which was still the region of highest SCF, when the collar height was reduced to around 50mm. However, in contrast to the behaviour of the full-scale connector, the large difference in stiffness between the outside and inside surfaces due to the presence of the collar, produced a high secondary bending stress component that produced a tensile stress on the inside surface. The importance of this became apparent when fatigue tests were performed on trial strip specimens with ~50mm high collars, one of which failed near the grips from the inside surface. Since, in reality, actual connectors are more likely to fail from the stress concentrating features on the outer surface, this design was considered to be unsuitable.
Further FE modelling indicated that complete removal of the collar, leaving that region flush with the neighbouring outside surface, reduced the bending stress induced by the thickness change considerably, without significantly changing the SCFs on the outside surface. This can be seen in Figure 4, which compares the FEA stress contours for the partial (Fig. 4(a)) and complete (Fig. 4(b)) removal of the collar. Complete removal of the collar has slightly reduced the SCF at the thickness transition radius, from 1.47 to 1.30, but this still remains as the region of maximum SCF. Therefore, this specimen design, which is shown in Figure 3, was the one finally adopted. It possessed the particular features of retention of the original surface finish and geometry, and hence SCFs at the critical locations, and reduction of the secondary bending stress.
3.2.2 Surface finish
Two types of surface finish were adopted for the strip specimens. One represented the surface condition after the machining of a connector, corresponding to a surface roughness of 3.2mm in Ra, and this was applied to the specimens from Connector L. The other represented the surface condition prior to coating, 8.1mm in Ra, and this was applied to the specimens from Connector H. However, the edges of all the strip specimens were carefully ground longitudinally to prevent premature failure from the edge.
3.2.3 Strain gauging
Most specimens were instrumented with strain gauges in the regions of the expected failure location, as indicated in Figure 3. The resulting maximum SCFs, usually at the thickness transition, are recorded in Table 1. In general, they were comparable with those estimated by FEA.
3.2.4 Fatigue testing
The specimens were tested under constant amplitude tensile axial loading in a 1000kN servo-hydraulic fatigue testing machine at a frequency of 2-5Hz in laboratory air at ambient temperature. Two pairs of packers were used in gripping the ends of each specimen with wedge jaws. Two stress ratios (R = σmin/σmax) were used, 0.1 and 0.4, and stress ranges were selected to cover the endurance range 105 to 2x106 cycles.
3.3 Small cylindrical specimen
3.3.1 Specimen design
Standard uniform-gauge test section cylindrical specimens were used for both low- and high-cycle tests. In the former the gauge diameter d was 6mm and the gauge length l was 14mm. In the latter, both d and l were greater (d=8mm and l=25.4mm) to facilitate fatigue testing using an Amsler Vibrophore fatigue test machine. The specimens for both test types were machined to give a surface finish corresponding to 3.2μm in Ra in the longitudinal direction.
3.3.2 Low-cycle fatigue (LCF) tests under strain control
The local strain fatigue analysis method requires the cyclic properties of the material. These were produced from LCF tests performed under strain control in a 100kN servo-hydraulic universal testing machine, the strain being controlled using an extensometer. The tests were conducted in air at 22°C, at a strain ratio (minimum strain/maximum strain) of R=–1 and a strain rate of 60.0%/minute. A total of ten tests were performed in accordance with BS 7270 (6). The fatigue endurance was defined as 10% drop of the maximum stress in a stabilised cyclic loop.
3.3.3 High-cycle fatigue tests under load control
The aim of the high-cycle fatigue (HCF) tests was to investigate the extent to which such relatively simple tests could be relied upon to establish the fatigue strength of a large forging. Furthermore, the results can supplement the LCF data at long endurance where elastic strain is predominant. A total of ten tests were conducted in line with the guidance (7). The specimens were tested in an Amsler Vibrophore fatigue test machine at a stress ratio R=0.1 and a frequency of ~130Hz. Since the upper yield strength of the material was about 536MPa, the maximum stress was kept below this value in order to avoid plastic collapse of the test specimen.
4. Fatigue Test Results
4.1 Strip specimens
4.1.1 Fatigue tests
The test results obtained from the strip specimens are summarised in Table 1. The table also provides information about failure location, the maximum SCF obtained from the strain gauge measurements in the specimen gauge section (or from FEA if not instrumented) and the corresponding local stress range, nominal x SCF. It should be noted that, although majority of these SCFs corresponded to the failure sites, they represented the maximum values in the specimens when failures occurred at locations out of the gauge section (for example, on the inside surface, or the gripping area). Fatigue failures occurred predominantly on the outside surface in the specimen gauge section, ie, the area with the smallest WT and specimen width on each side of the removed collar.
The fatigue lives of all strip specimens, including those that either ran-out or failed outside the gauge section, are plotted in Figure 5 in terms of local stress range. Referring to Figure 5, it will be evident that, for each R value, there was no noticeable difference in fatigue performance between the two connectors, indicating that the difference in their surface finish, 3.2 compared with 8.1mm, was not significant. The BS 7608 Class B mean and design curves (1) are also included in Figure 5 for comparison. It can be seen that all the results exceeded the Class B mean curve, especially in the long life regime (>106 cycles). Fatigue strength is often expressed as an S-N curve with the following form:
where A and m are constants characterising the S-N curve. Curves of this form were fitted to the valid test results for each R value in Table 1 by regression analysis. On the basis that surface finish differences had no significant effect on fatigue performance, the results from the two connectors were combined for this analysis. The resulting values of the parameters A, m and standard deviation (SD) of log(N) determined for each R value are given in Table 2 and the best-fit curves are shown in Figure 5. It can be seen that the fatigue endurance at R=0.4 was consistently lower than that for R=0.1, notably in the long life regime. Qualification of a specific design S-N curve on the basis of a limited number of test results can be justified with 95% confidence if the mean curve fitted to the test results exceeds the following target curve (8):
where AM and SD are the constant and standard deviation of log(N) associated with the mean curve for the design curve to be qualified, and, in this context, n is the number of test results. The SD was 0.182 and the value of 1.645 is obtained from standard normal probability tables at a confidence of 95%. By taking the same slope as the Class B design curve and assuming a sample size of eight (this was the number of valid test results for R=0.4;. it was 14 for R=0.1), the target curve to support Class B is also included in Figure 5. Since all the test results, including those from specimens that either ran-out or failed outside the specimen gauge section, exceeded this target curve, it can be concluded that the data meet Class B at the selected confidence level. With increasing sample size, the target curve will merge with the Class B mean curve.
4.1.2 Failure locations and investigation
Fatigue cracking in most specimens initiated at the thickness transition location on the outside of the original connector surface where the highest SCF was predicted by FEA. Figure 6 shows an example. A striking feature of the forging material was that fatigue cracking sometimes initiated from a subsurface defect as shown in the example in Figure 7 (marked with number '1'). The defect was identified to be an aluminium oxide inclusion using energy dispersive spectrum (EDS) analysis.
Figure 8 compares the endurances of those specimens failing from a subsurface inclusion with those of the specimens failing from the specimen surface. As will be seen, there is no significant difference between them in the case of the data obtained at R=0.1. For the tests conducted at R=0.4, only one specimen failed from an inclusion and its endurance appeared to be on the lower bound of the data for that stress ratio.
4.2 Small cylindrical specimens
4.2.1 Strain controlled tests
For each specimen tested, the elastic and plastic strain amplitudes in the cyclic loop were determined at half of its endurance, where the cyclic hysteresis loops were considered to be stabilised. The results from the ten specimens tested under strain control are summarised in Table 3. Figure 9 shows an example of the tensile stress-strain curve and the hysteresis loop in the first cycle. The LCF data are also plotted in Figure 10 in terms of strain amplitude against number of reversals to failure, 2Nf.
Based on the LCF test results, and by using Neuber’s rule (9) to relate the local stress/strain ranges with the remote stress/strain ranges, the cyclic properties of the material were determined (10) and are given in Table 4.
4.2.2 Load controlled tests
The results obtained from the small cylindrical specimens tested under load control are summarised in Table 5. Only three of the ten specimens tested failed in the gauge section, with the remainder either failing from the thread in the specimen gripping area (treated as run-outs) or remaining unbroken. Figure 11 compares these test results with those obtained from the strip specimens at the same stress ratio (R= 0.1), together with the Class B mean S-N curve. As can be seen, all the results are above the Class B mean curve. Allowing for scatter in the larger number of strip specimen results, the two specimen types have given very similar fatigue performance.
5. Analyses of the Fatigue Test Results
5.1 Strip specimens
The fatigue test results obtained from the strip specimens were assessed as the basis for the fatigue design of full-scale forged components, with particular reference to SCRs. In this context, it is often necessary to consider higher tensile mean stress conditions than those investigated here. To illustrate a possible approach to fatigue design under higher stress ratios, the present results from strip specimens were analysed using the well-known Goodman correction. Goodman proposed the following equation to relate fatigue endurance limits at different mean stresses:
where σUTS is the tensile strength of the material, ΔσR=-1 is the fatigue limit at R=-1 and ΔσR is the fatigue limit to be estimated for constant amplitude cyclic loading with a mean stress of σm.
The strip specimens were only tested at R=0.1 and R=0.4, not at R=-1. Therefore, the above Goodman expression was modified to calculate the fatigue limit at a higher mean stress, σm,R, using as reference the experimental data obtained at R=0.1, as follows:
Since 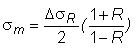 , the above equation is equivalent to:
, the above equation is equivalent to:
It should be pointed out that the derivation of the above equation relies on the assumption that the fatigue data obtained at R=0.1 are consistent with the Goodman equation.
To verify the Goodman equation, the fatigue limit for R=0.4 was calculated using Equation [5], together with the mean fatigue limit obtained at R=0.1, and compared with the experimental value. The present fatigue tests were not designed specifically to determine fatigue limits. However, these can be estimated on the basis of extrapolation of the S-N curves fitted to the results. It is generally found that the fatigue limit for a smooth specimen corresponds to the applied stress range at an endurance of between 2x106 and 107 cycles on the S-N curve fitted to the results obtained from failed specimens, depending on the type of specimen. Comparison of the mean curves and the experimental data in Figure 5 suggests that 107 cycles would be a reasonable choice for the present specimens. On this basis, the estimated fatigue limits obtained from the fitted mean S-N curves are 413MPa for R=0.1 and 283MPa for R=0.4. Recalling that the specified minimum σUTS of the present forgings was 552MPa, and noting that a stress range of 413MPa at R=0.1 corresponds to σm,R=0.1 = 252MPa, from Equation [6] Ω = 761MPa. Thus, from Equation [5]:
It is considered that this agrees sufficiently well with the experimental value of 283MPa to validate the Goodman correction.
On this basis, the estimated fatigue limit for R=0.8 is 106MPa, a considerable reduction. Indeed, it may be noted that this value is lower than the mean Class B fatigue limit and approaches the design value of 100MPa. In view of this there is a clear need for fatigue design data that are related to the applied mean stress or stress ratio. This contrasts with the current approach using Class B in conjunction with the applied stress range regardless of mean stress, on the basis that the design curve already includes the most harmful influence of mean stress.
The analysis so far has produced estimates of the effect of applied stress ratio on the constant amplitude fatigue limit. In practice, corresponding S-N curves are required. There does not seem to be an accepted relationship, comparable with the Goodman equation, between fatigue strength and stress ratio that could be used to estimate such curves. However, what is clear is that S-N curves obtained at different stress ratios converge in the low-cycle regime. Logically they should approach some critical stress value, such as yield or σUTS. However, in practice it is not so simple and S-N curves in the low endurance regime are not easily correlated, due to such factors as stress redistribution at stress concentrations, material changes at high stress and even deviation from a linear S-N curve. Therefore, in the present exercise it was decided to locate the convergence point on the Class B S-N curve. Taking the experimental data shown in Figure 5 as a guide, convergence at N=2x104 cycles seems reasonable. This is illustrated in Figure 12, which compares the experimental data and calculated S-N curves based on the fatigue limits deduced using the Goodman equation and convergence at N=2x104 cycles on the Class B mean S-N curve.
It will be noted from Figure 12 that the Class B curve coincides with the calculated curve for R=0.76. This seems entirely reasonable since, as noted earlier, the Class B curve was derived from fatigue test data obtained from welded specimens containing very high tensile residual stresses. These would have had the effect of producing a very high effective stress ratio for any applied cyclic stress. Of course, the Class B database specimens did not have the good surface finish achieved in the present steel forgings. However, it is not inconceivable that surface finish has less effect on fatigue performance under high stress ratios.
Thus, it is suggested that the approach used to calculate the S-N curves in Figure 12 is a suitable basis for the fatigue design of steel components. In particular, the current Class B design curve would be retained as the appropriate one for high applied tensile mean stresses or stress ratios, specifically for R ≥ 0.76. Then, S-N curves for lower R values would be calculated as follows:
a) Taking the Class B design curve as reference and assuming that it applies for R=0.76, the design fatigue limit, ΔσR=0.76, is 100MPa, at which σm,R=0.76 = 367MPa. Thus, from Equation [6], Ω = 100/(1 - 367/σUTS). Using as an example the present forgings, for which the specified minimum σUTS is 552MPa, Ω = 298MPa.
b) Equation [5] is then used in conjunction with this Ω value to calculate the design fatigue limits for other R values. Following the example of the present forgings,
Then, for example, ΔσR=0.1 = 224MPa and ΔσR=0.4 = 183MPa.
c) The S-N curve for the required R value is constructed on the basis that it joins the co‑ordinates, on a log-log diagram, ΔσR at 107 cycles and 474MPa at 2x104 cycles, where it meets the Class B design curve. Expressing the equation of the required S-N curve as Equation [1], the constants m and A can be obtained from:
Following the above example, ΔσR=0.1 = 224MPa, in which case m=8.30 and A = 3.23x1026. Figure 13 illustrates possible design curves for various R values, including R=0.1 and 0.4, in comparison with the present experimental data. It can be seen that each set of data lies well above the corresponding design curve.
5.2 Life predictions based on the local strain approach
The local strain approach relates deformation occurring in the immediate vicinity of a stress concentration to the remote stresses and strains using the constitutive response determined from fatigue tests on simple laboratory specimens. Thus, by combining both the Basquin and Coffin-Manson (11,12) equations, the fatigue life of a notch is related to the total strain range. Fatigue life prediction using the local strain approach was composed of the following steps:
- Determination of cyclic stress-strain curve
A stabilised cyclic stress-strain curve of a material can be described by the following equation:
where
εe is elastic strain amplitude
εp is plastic strain amplitude
n' is cyclic strain hardening exponent
K' is cyclic strength coefficient
- Determine the relevant parameters in the Basquin and Coffin-Manson equations
Basquin’s equation correlates fatigue endurance with elastic strain range. It is expressed as:
The Coffin-Manson equation correlates fatigue endurance with plastic strain range. It is expressed as:
where
Δεe and Δεp are respectively elastic and plastic and strain range;
2Nf is number of reversals to failure (1 cycle = 2 reversals);
σf' is fatigue strength coefficient
b is fatigue strength exponent
εf' is fatigue ductility coefficient
c is fatigue ductility exponent
By plotting the elastic and plastic strain ranges against number of reversals, the above four material parameters were determined and are shown in Table 4.
- Determination of local strain at a notch
The local strain approach relates deformation occurring in the immediate vicinity of a stress concentration to the remote stresses and strains using the constitutive response. Neuber’s rule (9) relates the local stress/strain ranges with the remote stress/strain ranges by:
where Kt is SCF and ΔS is nominal stress range. Equation 12 was modified by Topper et al (13) as:
where Kf is fatigue notch factor. Peterson (14) proposed the following equation for estimating Kf of a material:
where ρ is the radius at a notch, an is a material parameter and is related to the tensile strength, σuts, of the material. Peterson proposed (15):
The strain amplitude v number of reversals to failure curve predicted using the parameters in Table 4 is compared with the LCF test results in Figure 10. The prediction agrees well with the experimental data, verifying the correctness of these parameters.
Morrow (16) modified the above Coffin-Manson equation, which refers to R=-1, to take account of mean stress:
The resulting endurance curve predicted using this equation for R=0.1 is shown in comparison with the experimental data in Figure 14. As these specimens were loaded in the elastic regime, the stress ranges were converted to strain ranges using Hooke's law. Good agreement was again found between the experimental data and the prediction for R=0.1.
The cyclic material properties were then used to calculate the fatigue performance of the strip specimens. Each local stress range from the strip specimen was converted to strain range using Neuber’s rule. The predicted curve is shown in comparison with the experimental data in Figure 15. It will be seen that it is in reasonable agreement with the mean curve fitted to the data for R=0.1, but not for R=0.4. Judged ‘by eye’, the predicted line might be accepted as a reasonable fit to the test results but the slope of that line was found to be outside the range of possible values based on the confidence limits on the estimated slope of the mean curve fitted to those results by regression analysis. In other words, there is a very low probability that an S-N curve fitted to the experimental data has such a shallow slope as the predicted line. It would seem that a mean stress correction is required that changes the slope of the predicted line as well as its position.
6. Comparison with data from Norsk Hydro TLP forgings
Fatigue testing of several high-strength quenched and tempered (QT) steels for tension leg platform (TLP) application was performed by Veritec on behalf of Norsk Hydro (17). The testing programme was to establish the S-N design curve for these steels and to investigate the effects of steel tensile strength and surface roughness on fatigue performance. Since both the strengths and surface finish of these QT steels were similar to that of the steel forgings investigated in this paper, and the tests were conducted at several different stress ratios, an opportunity was taken to examine the S-N curves proposed using these test data. It is noted that the DNVGL-RP-C203 HS (high strength) S-N curve is based on these fatigue test data.
The programme involved forgings from three manufacturers and various specimen types (plates with and without a notch, cylindrical), surface finish conditions and loading conditions, as summarised in Table 6. For each set of fatigue testing, fatigue tests were conducted at three different stress levels. Most tests involved cycling down from a fixed high tensile stress (500MPa), so that R increased with decrease in applied stress range.
The Veritec fatigue data are compared with those from the strip specimens in Figure 16. It should be borne in mind that, as noted above, results from the Veritec data that were produced with constant maximum stresses resulted in stress ratios that varied from around R=0.1 at higher stress ranges and R=0.4 at low. However, the present tests on the strip specimens were performed at two constant stress ratios. It can be seen from Figure 16 that all the endurance data obtained in the Veritec testing programme exceeded the Class B design curve, especially in the long life regime.
Noting that the Veritec database includes many results obtained from un-notched specimens with a similar surface finish to the present specimens and tested at the two stress ratios used in the present investigation, R=0.1 and 0.4, the value of combining the data was explored. Of particular interest was any indication that the data used to develop the proposed design approach in Section 5.1 may be invalid. At the same time, it was an opportunity to check the proposed design S-N curves for these two stress ratios. The relevant results for the two stress ratios are shown in Figure 17, together with the Class B design curve and the proposed curve for the appropriate stress ratio. In the case of the larger number of results obtained at R=0.1, Figure 17a), combining the present strip and high-cycle fatigue data with those from the Terni and JSW specimens results in a mean S-N curve very similar to that fitted to the strip specimen data alone. Thus, these extra data support the basic S-N curve used in the derivation of the design approach. However, adding the Bjørneborg results leads to very poor correlation between the data and an estimated mean S-N curve that is clearly far too steep. This is undoubtedly a reflection of the disproportionate influence of the large number of results obtained at a single stress level. Combining the available data obtained at R=0.4, Figure 17(b), had a similar effect, for the same reason. Thus, the extra data are generally in agreement with the present results, but considering them in the derivation of the proposed design approach in Section 5.1 would have been difficult and would not have justified any significant changes to the final proposed design approach. Furthermore, all the extra data lie above the proposed design curves.
7. Discussion
Designers of mechanical connectors use or reference the Class B design curve as the lower bound for their analyses. As noted earlier, in contrast to the design curves that relate to welded joints, this design curve was not based on fatigue data obtained from representative specimens. Data from the plain steel specimens had been considered in the original evaluation of fatigue test results (18), but the resulting potential design curve was considered to be too high in comparison with data obtained from structural components. Instead, it was decided to base the design S-N curve for plain unwelded steel on fatigue data obtained from the highest fatigue strength weld detail, that is the longitudinal butt weld. Comparison with the present experimental data, as well as those from other sources, did not support the general application of Class B for fatigue design of machined components such as the present forged steel connectors. It is too conservative in the long life regime if the applied stress ratio is low.
Based on the analyses of the experimental data from the strip specimens, an alternative design approach has been developed for smooth components like the forgings tested. This takes Class B as the basic design curve for high stress ratios, R≥0.76, but introduces higher curves for lower R values, derived on the basis of the increase in fatigue limit with reduction in R according to the Goodman correction. Compared to the experimental data from Veritec, the recommended design approach is conservative and appears appropriate. However, this approach was developed on the basis of rather few test results. Clearly, further experimental support is required, including from fatigue tests on suitable small- and full-scale specimens with a wider range of surface finishes and applied stress ratios than those investigated here, to confirm it.
When Goodman’s expression was used to account for the effect of mean stress, the specified minimum sUTS (552MPa) of the forgings was used since the actual sUTS of the material was not available. However, the low cycle fatigue tests suggested that it was greater than 573MPa. It should also be noted that the tensile strength of the Bjørnborg specimens (17) was 627MPa. By assuming sUTS=600MPa, the fatigue limit at R=0.4 was estimated to be 299MPa, slightly greater than 292MPa estimated based on the specified minimum σUTS of 552MPa. The following can be seen from this analysis: (1) the effect of tensile strength on the estimated S-N curve is small; (2) use of the estimated S-N curve is conservative when used for steels with sUTS greater than 552MPa. Furthermore, it should be noted that design for static failure is commonly based on a stress between sy and σUTS of material. If design is based on yield strength, then the σUTS in Equation [3] should be replaced by the material’s σy, ie the Soderberg’s equation should be used.
The local strain approach proved to be effective for predicting the fatigue strengths at R=0.1 for both the small cylindrical specimens under load control and the strip specimens. However, the method was un-conservative when applied to the strip specimens tested at R=0.4 for endurances beyond 106 cycles. Furthermore, the slopes of the predicted curves were all similar for different stress ratios, which was contrary to the experimental observation that they became steeper as the mean stress increases. This inadequacy of Morrow’s expression suggests that its application should be limited to the calculation of fatigue strengths for modest mean stress levels, or to the short life regime (less than 106 cycles) for the material. This is consistent with the observation made elsewhere that the local strain approach is not necessarily applicable to long life situations where surface finish and other processing variables are known to have a large effect (19).
Only three of the HCF tests of the small cylindrical specimens produced failure in the gauge section, too few to derive an S-N curve. However, in spite of this rather limited number of results, it seems reasonable to conclude that the fatigue performance of these specimens was not significantly different from that of the strip specimens tested at the same stress ratio, Figure 11. This is not altogether surprising given that they had similar surface finish and neither type of specimen contained a notch.
It has been generally recognised that, all other factors being equal, the fatigue performance of a component, from the point of view of failure from the surface, depends on its surface finish, the finer the surface finish the better the fatigue performance. Clearly, it would be useful to quantify this effect as well as that of applied stress ratio in the proposed new design approach. A possible method would be to adopt the surface finish correction procedure included in the European pressure vessel design rules, EN 13445 (20). This takes the form of a fatigue strength reduction factor, ƒs, that is applied to the design S‑N curve and is given by:
and Rz is the average of ten largest peak-to-valley heights (in μm) within the region assessed. To check the validity of the correction procedure, it can be applied to the present strip specimens. For these, the values of Rz were ~13μm for the strip specimens from Connector L and ~46μm for those from Connector H. By assuming that the roughness‑induced life reduction factor for the specimens from Connector L was unity, the relative life reduction factor for the specimens from the Connector H was calculated and the result is plotted in Figure 18. In the short life regime (100 cycles), roughness variation has no effect on endurance. The fatigue strengths of the specimens with rougher surface finish were predicted to decrease with increasing endurance, resulting in a fatigue strength reduction factor of about 0.9 at a fatigue endurance of 107 cycles. This indicates that, according to EN 13445, the surface finish effect on fatigue performance in this investigation is not expected to be significant, as indeed was the case. A wider variation in fatigue performance would be expected for a larger range of surface roughness. This is illustrated in Figure 18, which includes the correction recommended for as-rolled or extruded steel, the roughest surface referred to in EN 13445. Clearly, this surface finish correction could be used in conjunction with the proposed new design approach, taking a surface with around 10mm in Ra as the reference value.
It seems reasonable to assume that many of the structural components that provided the database in Figure 1 had surfaces that were comparable with as-rolled or extruded steel. As seen in Figure 18, the maximum fatigue strength reduction factor is now around 0.8. The basis of the correction in EN 13445 is not known. It may not be suitable for the range of surface finishes considered here, or there may be other features, such as distinct surface imperfections, in the lower fatigue strength structural components that over-ride any significance of the surface finish. This is an issue that requires further study.
Finally, it should be emphasised that all the fatigue data and design recommendations presented here refer to constant amplitude loading. In practice, components and structures experience variable amplitude loading. The most widely used design approach in such circumstances is to use Miner's rule in conjunction with the constant amplitude S-N curve extrapolated beyond the fatigue limit at a shallower slope, usually m+2. This modification of the S-N curve is introduced to allow for the fact that stresses below the fatigue limit become damaging once a fatigue crack has initiated and started to propagate. The approach was developed on the basis of the fatigue behaviour of welded joints, where the majority of the life consists of crack propagation. The situation is different in the case of fatigue in plain, unwelded, materials in that crack initiation can occupy the majority of the fatigue life, depending on the severity of the stress concentration feature at which the crack initiates. In such cases, the potential damage from stresses below the fatigue limit will be less than in welded joints, making the design approach too conservative. However, in the absence of variable amplitude fatigue test results for plain steel components to confirm this, it is recommended that the approach is retained.
8. Conclusions
This study addressed the problem of designing large steel components with respect to potential fatigue failure in the steel. Particular attention was focused on forged steel connectors of the kind used in steel catenary risers and the validity of the Class B S-N curve for their design. On the basis of the results of fatigue tests performed on strip and small-scale cylindrical machined specimens extracted from two actual forged steel J-lay connectors, together with available published data obtained from specimens or structural components that failed in plain steel, the following conclusions can be drawn:
- The fatigue performance of all specimens tested exceeded the Class B design curve, which was particularly conservative for low stress ratios in the high-cycle regime.
- The fatigue strength of the forged steels considered decreased significantly with increases in applied tensile mean stress or stress ratio.
- The range of surface roughness investigated, 3.2 to 8.1μm in Ra, did not have a significant effect on fatigue performance. This was consistent with the correction factor for surface finish in the European pressure vessel standard, EN 13445.
- The local strain approach provided a reasonable estimate of the fatigue performance of the strip specimens at R=0.1. However, the method was not suitable for higher R values.
- Based on the strip specimen data and the Goodman mean stress correction, an alternative fatigue design approach that included the effect of applied stress ratio was developed. This accepted the current Class B curve but only for R ≥ 0.76, and then provided higher curves for lower R values. This design approach could be used in conjunction with the surface finish correction term from EN 13445.
- The present test results were reasonably consistent with available published fatigue data for forged steel specimens with similar surface finish. Better performance was obtained for a finer surface finish, especially in the long life regime. However, the published data were consistent with the proposed new design approach.
9. Acknowledgement
Sponsorship of this study by BP is acknowledged.
10. References
- BS 7608:2014: 'Code of practice for fatigue design and assessment of steel structures', BSI, London, 2014.
- Maddox S J and Razmjoo G R, 1998: 'Fatigue performance of large welded steel tubes', Proc. 17th International Conference on Offshore Mechanics and Arctic Engineering (OMAE), ASME, New York.
- Maddox S J, 2001: 'Assembly of available fatigue data relevant to pressure equipment design', in Taylor N (Editor): 'Pressure components fatigue design in the framework of Directive 97/23/EC on pressure equipment', European Commission, NL-1755 ZG Petten, The Netherlands.
- Buitrago J, Weir M S and Kan W C, 2003: 'Fatigue design and performance verification of deepwater risers', Proc. 22nd International Conference on Offshore Mechanics and Arctic Engineering (OMAE), ASME, New York.
- Gurney T R, 1974: 'Revised proposals relating to fatigue design stresses', Welding Institute Report No. 3381/3/74, May 1974.
- BS 7270:1990: 'Method for constant amplitude strain controlled fatigue testing', British Standard Institution, London, UK, 1990.
- ASTM E466-96, 'Standard practice for conducting force controlled constant amplitude axial fatigue tests of metallic materials', ASTM, 1996.
- Schneider C R A and Maddox S J, 2004: 'Statistical analysis of fatigue data', TWI Best Practice Guide 13604.01/02/1157.02, February 2004.
- Neuber R E, 1961: Journal of Applied Mechanics, Vol.8, pp.544-550.
- Bannantine J A, Comer J J and Handrock J L, 1990: 'Fundamentals of metal fatigue analysis', Prentice-Hall, USA.
- Coffin L F, 1954: 'A study of the effects of cyclic thermal stresses on a ductile metal', Transactions of the American Society of Mechanical Engineers, 76, 931-950.
- Manson S S, 1953: 'Behaviour of materials under conditions of thermal stress', National Advisory Commission on Aeronautics: Report 170, Cleveland, Lewis Flight Propulsion Laboratory.
- Topper T H, Wetzel R M and Morrow J, 1969: Journal of Materials, Vol.4, pp.200.
- Peterson R E, 1974: 'Stress concentration factors', New York, Wiley-Interscience.
- Peterson R E, 1959: 'Analytical approach to stress concentration effect in fatigue of aircraft structures', WADS symposium, Wright Air Development Center, Aug. 1959.
- Morrow J, 1968: 'SAE fatigue design handbook', edited by Graham F, pp.21-30.
- Karlsen A et al, 1990: 'Additional material testing – Snorre tether elements', Veritec report No. 90-3199, 8 June 1990.
- Gurney T R and Maddox S J, 1973: 'A re-analysis of fatigue data for welded joints in steel', Welding Research International, 3 (4), 1973, pp.1-54.
- SAE, 1997: 'Fatigue Design Handbook', 3rd edition, AE-22, Society of Automotive Engineers, Inc., Warrendale, USA.
- BS EN 13445:2009: 'European standard for unfired pressure vessels', BS EN 13445:2009, BSI, London, 2009.
Table 1 Summary of fatigue test results from the strip specimen.
| Specimen No. |
Endurance, Nf |
Nominal stress range, MPa |
SCF2 |
Local stress range, MPa |
Stress ratio R |
Failure location |
Included in
regression
analysis |
| L-031 |
3.08E+05 |
387 |
1.37 |
530 |
0.1 |
On outside surface, within the specimen gauge section |
Yes |
| L-041 |
3.15E+05 |
350 |
1.37 |
480 |
0.1 |
On outside surface, out of the specimen gauge section |
No |
| L-05 |
3.15E+05 |
400 |
1.24 |
496 |
0.1 |
From an inclusion, within the gauge section |
Yes |
| L-09 |
3.18E+05 |
427 |
1.30 |
555 |
0.1 |
On outside surface, within the gauge section |
Yes |
| L-10 |
6.27E+06 |
325 |
1.20 |
390 |
0.1 |
Run out |
No |
| L-11 |
1.29E+05 |
450 |
1.26 |
567 |
0.1 |
From an inclusion near outside surface, within the gauge section |
Yes |
| L-14 |
1.34E+05 |
450 |
1.23 |
554 |
0.1 |
On the outside surface, within the gauge section |
Yes |
| L-15 |
1.30E+06 |
400 |
1.29 |
516 |
0.1 |
From an inclusion near the inside surface, within gauge section |
Yes |
| L-16 |
2.50E+05 |
427 |
1.26 |
538 |
0.1 |
From an inclusion near outside surface, within gauge section |
Yes |
| L-17 |
8.62E+04 |
470 |
1.19 |
559 |
0.1 |
On outside surface, within the gauge section |
Yes |
| H-01 |
1.02E+05 |
427 |
1.25 |
534 |
0.1 |
On outside surface, within the gauge section |
Yes |
| H-02 |
1.86E+05 |
400 |
1.29 |
516 |
0.1 |
On outside surface, within the gauge section |
Yes |
| H-03 |
1.61E+05 |
450 |
1.30 |
585 |
0.1 |
On outside surface, within the gauge section |
Yes |
| H-04 |
1.94E+06 |
375 |
1.30 |
488 |
0.1 |
From an inclusion, within specimen gauge section |
Yes |
| H-05 |
5.35E+06 |
350 |
1.30 |
455 |
0.1 |
Run out |
No |
| H-06 |
6.65E+04 |
470 |
1.30 |
611 |
0.1 |
On outside surface, within the gauge section |
Yes |
| H-07 |
2.83E+06 |
387 |
1.30 |
503 |
0.1 |
From an inclusion near outside surface, within gauge section |
Yes |
| L-06 |
1.51E+06 |
267 |
1.38 |
368 |
0.4 |
On outside surface, within the gauge section |
Yes |
| L-07 |
2.18E+06 |
247 |
1.30 |
321 |
0.4 |
From an inclusion near inside surface, within gauge section |
Yes |
| L-08 |
3.02E+06 |
280 |
1.26 |
353 |
0.4 |
At the clamping area |
No |
| L-12 |
2.92E+06 |
300 |
1.24 |
372 |
0.4 |
On outside surface, within gauge section |
Yes |
| L-13 |
3.41E+05 |
320 |
1.23 |
394 |
0.4 |
On outside surface, within gauge section |
Yes |
| L-18 |
3.99E+05 |
320 |
1.30 |
416 |
0.4 |
Multiple cracking on outside surface, within gauge section |
Yes |
| H-08 |
2.12E+05 |
320 |
1.30 |
416 |
0.4 |
Multiple cracking on outside surface, within gauge section |
Yes |
| H-09 |
4.66E+05 |
300 |
1.30 |
390 |
0.4 |
On outside surface, within the gauge section |
Yes |
| H-10 |
2.55E+06 |
280 |
1.30 |
364 |
0.4 |
Run out |
No |
| H-11 |
4.07E+05 |
290 |
1.30 |
377 |
0.4 |
On outside surface, within the gauge section |
Yes |
Notes: 1: The specimen design for all specimens is shown in Figure 3. The thickness at the central part was 49.2mm for specimens L-03 and L-04, but 32.5mm for the remaining specimens.;
2. For specimens instrumented with strain gauges, the SCF was the value determined from strain gauges. For specimens without strain gauges, a SCF value 1.30, determined from FEA, was used (shown in bold).
Table 2 Results of regression analysis for fitting S-N curve to strip specimen data
Stress ratio |
Connector |
Sample size |
Amean |
Exponent m |
SD |
| R=0.1 |
L + H |
14 |
2.67 x 1042 |
13.54 |
0.349 |
| R=0.4 |
L + H |
8 |
1.31 x 1029 |
9.02 |
0.295 |
Table 3 LCF test results from the small cylindrical specimens tested under strain control
| Fatigue tests under strain control |
| Specimen No. |
Strain amplitude |
Young's modulus, MPa |
Endurance, Nf, cycles |
Elastic strain amplitude |
Plastic strain amplitude |
| 4560 |
5.00E-03 |
203,200 |
2,395 |
0.0024 |
0.0026 |
| 4561 |
2.50E-03 |
206,600 |
32,163 |
0.0002 |
0.0023 |
| 4562 |
1.00E-02 |
203,400 |
309 |
0.0070 |
0.0030 |
| 4563 |
2.00E-03 |
206,100 |
288,463 |
0.0001 |
0.0020 |
| 4564 |
3.50E-03 |
205,100 |
4,841 |
0.0010 |
0.0025 |
| 4565 |
5.00E-03 |
207,700 |
1,954 |
0.0024 |
0.0026 |
| 4566 |
3.50E-03 |
205,800 |
6,655 |
0.0010 |
0.0026 |
| 4567 |
7.50E-03 |
202,600 |
572 |
0.0046 |
0.0030 |
| 4568 |
7.50E-03 |
208,400 |
401 |
0.0048 |
0.0028 |
| 4569 |
2.50E-03 |
205,700 |
25,111 |
0.0003 |
0.0023 |
Table 4 Cyclic properties of forged steel determined from the LCF tests
| Young's modulus, MPa |
Average yield strength, MPa |
Cyclic strength coefficient K' |
Cyclic strain hardening exponent n' |
Fatigue strength coefficient σf' |
| Static |
Cyclic |
| 203,000 |
195,000 |
536 |
761 |
0.073 |
876 |
| Young's modulus, MPa |
Fatigue strength exponent b |
Fatigue ductility coefficient εf' |
Fatigue ductility exponent c |
| Static |
Cyclic |
| 203,000 |
195,000 |
-0.063 |
0.688 |
-0.709 |
Table 5 HCF test results from the small cylindrical specimens tested under load control
| Specimen No. |
Stress range, MPa |
Endurance, Nf, cycles |
R Ratio |
Failure location |
| S-01 |
400 |
1.40E+06 |
0.1 |
From threaded end |
| S-02 |
420 |
3.21E+06 |
0.1 |
From threaded end |
| S-03 |
450 |
1.23E+06 |
0.1 |
From threaded end |
| S-04 |
450 |
2.00E+07 |
0.1 |
Run out |
| S-05 |
475 |
6.10E+05 |
0.1 |
Specimen gauge section |
| S-06 |
465 |
1.04E+07 |
0.1 |
From threaded end |
| S-07 |
475 |
3.49E+05 |
0.1 |
Specimen gauge section |
| S-08 |
465 |
5.925+06 |
0.1 |
From threaded end |
| S-09 |
470 |
5.73E+06 |
0.1 |
From threaded end |
| S-10 |
475 |
4.10E+05 |
0.1 |
Specimen gauge section |
Table 6 Summary of some details of the Veritec testing programme relevant to the present project (Karlsen et al, 1990).
| Activity |
Manufacturer |
Yield / tensile strengths, MPa |
SCF |
Surface roughness, Ra, μm |
Number of specimens tested |
Maximum cyclic stress applied, MPa |
| 1 |
Bjørneborg |
515/627 |
1.0 |
3.2 |
80 |
500 |
| 2 |
Bjørneborg |
515/627 |
1.8 |
3.2 |
20 |
Varied, 500-650 |
| 4 |
JSW steel |
563/616 |
1.0 |
3.2 |
20 |
500 |
| 5 |
Ternil |
Varied, 500-609/ 641-720 |
1.0 |
0.16 - 0.24 |
20 |
varied |
| 10 |
Bjørneborg |
515/627 |
1.0 |
0.16 - 0.24 |
10 |
500 |
Figure 1 Fatigue test results obtained from pressure vessels, pipes, forging and plate that all failed in the plain steel remote from any welds (2-4).
Figure 2 Forged steel connectors from which test specimens were extracted (courtesy of BP).
Figure 3 Design of strip specimens. Specimens L-03 and L-04 were prepared with the collar partly removed to give a thickness of 49.2mm. The remaining strip specimens were prepared with the whole collar removed, to give a thickness at the collar of 32.5mm.
Figure 4 FE prediction of the axial stress (same as the maximum principal stress) distribution for the two designs of the strip specimen:
a) 49.2mm thick at the collar (the collar being partly removed);
b) 32.5mm thick at the collar (the collar being completely removed).
Figure 5 Comparison of the test results (all data in Table 1 were included) of the strip specimens with the Class B mean and design curves. The Class B target curve for an assumed sample size of eight is also included for comparison. The data with an arrow indicates run-out.
Figure 6 Typical fracture surface, showing crack initiation on the outside surface of a strip specimen, (specimen L-12).
Figure 7 An example of fatigue failure from an inclusion (specimen H-04). In this example, the inclusion was about 0.8mm long, 0.2mm high and 2.3mm from the outside surface.
Figure 8 Comparison of the fatigue performance of the specimens failing from an inclusion with that of the specimens failing from specimen surfaces.
Figure 9 An example, showing the tensile stress-strain curve and the first cyclic hysteresis loop (specimen 4560).
Figure 10 LCF test results for small cylindrical specimens tested under strain control.
Figure 11 Comparison of the fatigue endurances for the strip and small cylindrical specimens tested under load control, all at R=0.1 (local stress for the strip specimens and nominal stress for the small cylindrical specimens).
Figure 12 Comparison of the fatigue performance at R=0.4 between the experimental data and the prediction based on the experimental data at R=0.1 and the Goodman’s equation.
Figure 13 Examples of design curves for plain steel operating at different stress ratios based on proposed method of deriving design S-N curves from the Class B curve and the Goodman mean stress correction.
Figure 14 Comparison of the predicted S-N curves with the experimental data of the small cylindrical specimens at R=-1 and R=0.1.
Figure 15 Comparison of the predicted mean S-N curves, based on the LCF properties of the material, with the experimental data of the strip specimens at R=0.1 and R=0.4 (local stress for the strip specimens and nominal stress for the small cylindrical specimens).
Figure 16 Comparison of the present fatigue test data and published data for QT steel forgings (17). The nominal stress was used for specimens with SCF=1.0 while the local stress was used for specimens with SCF>1.0.
b)
Figure 17 Comparison of the present results, published QT forging data (17), the proposed design curves and the Class B design curve: a) R=0.1; b) R=0.4. The nominal stress was used for specimens with SCF=1.0 while the local stress was used for specimens with SCF>1.0.
Figure 18 Predicted relative fatigue strength reduction factor for the specimens with rougher surface finish (from Connector H) based on the guidance in BS EN 13445.