Effects of Mechanical Loading on Residual Stress and Fracture: Part II: Validation of the BS 7910:2013 Rules
Isabel Hadley and Simon Smith
TWI Ltd Cambridge, UK
Presented at Proceedings of the ASME 2014 Pressure Vessels & Piping Conference (PVP2014), July 20-24, 2014, Anaheim, California, USA.
Abstract
Failure of welded structures due to the presence of flaws is typically driven by a mixture of applied and residual stresses, yet in most cases only the former are known accurately. In as‑welded structures, a typical assumption is that the magnitude of welding residual stress is bounded by the room temperature yield strength of the parent material. The UK flaw assessment procedure BS 7910:2013 also assumes that mechanical loading (either as a result of proof testing or during the initial loading of an as-welded structure) will bring about a relaxation in residual stress. Conversely, the UK structural assessment code for nuclear structures, R6, contains a warning on the ‘limited validation’ of the BS 7910 approaches for stress relaxation and suggests that they should be used ‘with caution’. The aim of this study was therefore to review the basis of the BS 7910 clauses on stress relaxation with a view to harmonising the BS 7910 and R6 rules for cases in which the original welding residual stress distribution is not known.
A companion paper describes the history of the residual stress relaxation clauses of BS 7910. A considerable programme of work was carried out in the late 1980s to justify and validate the clauses, using a range of experimental and numerical work. This included analysis of work carried out by the UK power industry and used in the validation of the R6 procedure. The full underlying details of the work have not hitherto been available in the public domain, although the principles were published in 1988. The approach proposed in BS 7910 combines ‘global’ relaxation of residual stress (Qm) under high mechanical load with ‘local’ enhancement of crack tip driving force through the adoption of a simplified primary/secondary stress interaction factor, ρ. This is different from the method adopted by R6, but appears to be equivalent to allowing negative values of ρ under conditions of high primary stress.
A re-analysis of the original TWI work, using the current version of BS 7910, has shown nothing to contradict the approach, which represents a workable engineering solution to the problem of how to analyse residual stress effects in as-welded structures rapidly and reasonably realistically when the as-welded stress distribution is unknown.
1. Introduction
A companion paper 1 summarises the history of the treatment of welding residual stress by the UK fracture mechanics assessment procedure, BS 79102, and compares it with that of the R6 nuclear procedure3. In this paper, the BS 7910 stress relaxation rules are tested against experimental data and FE analyses that were available at the time (late 1980s), and recommendations are made for further validation of the approach.
The method given in clause 7.1.8.2 of the current (2013) procedure is to assume that the residual stress component, Qm, is the lower of either
where σ'Y is the yield strength of the ‘appropriate material’ at the assessment temperature (except that, for assessment temperatures below ambient, it is the room temperature value, ie σ'YRT, in Equation 1a, σ'f is the flow strength (average of yield and ultimate strengths) of the ‘appropriate material’ at the assessment temperature and σref is the reference stress.
2. Re-examination of the data presented by Leggatt (1988)
2.1 Experimental data
Leggatt4,5 reviews the results of a series of wide plate tests carried out by TWI and the CEGB (a forerunner of EDF Energy) and two pressure vessel tests carried out by CEGB and ORNL. All the wide plate tests featured flaws introduced artificially into parent material, so that tensile properties and fracture toughness could be considered consistent, and mechanical continuity (eg the absence of misalignment effects) ensured. In certain cases, residual stresses were introduced by thermal loading (CEGB tests) or by the introduction of a circular electron beam melt run around the area to be notched (TWI tests), and destructive techniques used to measure the magnitude of residual stress in the area of interest. A summary of the results is shown in Figure 1, taken from Leggatt’s work (slightly amended to remove extraneous information). This representation (PD 6493:1991 Level 3) is the closest match to Option 1 analysis using the current BS 7910:2013. The intention of the current work was to:
- Reproduce the analysis carried out by Leggatt,
- Re-interpret the datapoints using current BS 7910 methods, including global relaxation of residual stress where appropriate,
- Compare the results with an equivalent R6 analysis, where possible,
- Comment on whether the data support or conflict with the BS 7910 treatment of residual stress relaxation.
2.2 CEGB wide plate tests
The largest set of tests analysed by Leggatt was a series of 18 wide plate tests, reported by Formby 6 and Formby and Griffiths 7. The tests were carried out on thin-section steel plate with the specific intention of elucidating the effect of residual stress on fracture. Formby and Griffiths 7 postulated that residual stress would affect failure load at low temperatures (where brittle fracture would dominate failure) but have negligible effect at high temperatures, at which failure would occur predominantly by plastic collapse. To this end, they designed a series of tests on centre-cracked plates. Half of these (nine specimens) were tested to failure in the as-received condition, ie in the absence of residual stresses. Residual stresses were induced in the other half of the specimens via a thermal loading technique, with the residual stress distribution induced before the introduction of the crack. Test temperatures ranged from -196°C to room temperature, in order to provoke a range of behaviour from fully brittle to fully ductile. Leggatt’s FAD for the as-received specimens (ie those not subjected to residual stresses) shows nine datapoints, which are scattered around the Failure Assessment Line or FAL (see Figure 1; as-received specimens are designated by round black symbols other than those enclosed by ellipses).
Since the nine specimens subjected to residual stress were similar in all other respects to those without, a similar distribution of results (ie more-or-less evenly distributed around the FAL) would be expected for the specimens subjected to secondary stress, if the treatment of residual stress is correct. Leggatt’s analysis shows that, of the nine specimens subjected to residual stresses (indicated in Figure 1 by black squares), two lay on (or very close to) the FAL and seven lay slightly outside. Leggatt’s treatment of crack driving force includes the use of the primary/secondary stress interaction parameter, ρ. For information regarding fracture toughness, reference was made to the original works of Formby 6, and Formby and Griffiths 7. They commented that the fracture toughness determined ranged from 26MPa√m at -196°C to 195MPa√m (initiation toughness) at room temperature. For temperatures of -185°C and below, an apparent value of fracture toughness, KIca pp was used to allow for the effects of warm prestressing on fracture toughness. Formby 6 also comments that, for the low-temperature tests, the factor r is not needed because the occurrence of WPS would have reduced the plastic zone size during final fracture. They show analysis points for low-temperature failure both with and without the ρ factor.
The analysis carried out by Leggatt was reproduced from his data using the procedure extant at that time (PD 6493:1991), including, where appropriate, the residual stress relaxation rules (see companion paper1 for details). This is termed the ‘PD6493 method’. Results were plotted in terms of a BS 7910:2013 Option 1 FAD (similar to the PD6493:1991 FAD). A second set of calculations were then carried out using TWI’s CrackWISE® software, Version 5 (which automates the fracture and fatigue clauses of BS 7910:2013, including the stress relaxation rules (Equations (1a) and (1b)); this is termed the ‘BS 7910 method’. Finally, the measured residual stress (σRM) was incorporated into the analysis as a known membrane residual stress. These values were typically around 290N/mm2, but varied a little as a function of distance from the centre of the annulus as described by Formby6. This method is referred to as the ‘R6 method’. In all cases, the mean fracture toughness determined from SENB tests was used as the basis of Kmat, with certain values of Kmat corrected to take account of warm prestress effects as discussed. Primary/secondary stress interaction was analysed via the simplified ρ factor.
Results of the analyses are summarised in Figure 2 (as‑received specimens) and Figure 3 (specimens incorporating residual stress), from which it is apparent that:
- For the as-received (AR) specimens, the results reported by Leggatt4,5 and those derived using BS 7910:2013 are very close, certainly within 10% of each other in terms of both Kr and Lr. All that this shows is that the assumptions made in re-creating Leggatt’s graph, based on the work of Formby 6, are essentially correct and that the analysis procedure for components subjected to primary stress only has not changed significantly.
- Analysis points associated with the as-received specimens lie scattered along and around the Failure Assessment Line (FAL), as would be expected when using best estimates of materials properties and accurate measurements of failure conditions.
- For the specimens containing residual stress, there is a reasonable correspondence between the results shown by Leggatt 4 (based on PD 6493:1991) and those derived using BS 7910:2013, allowing stress relaxation as per Equations (1a) and (1b). The discrepancy (of up to 20% in Kr) between Leggatt’s results and those calculated from BS 7910:2013 is due mainly to the change in the assumptions made regarding residual stress relaxation between the two procedures, as discussed in the companion paper 1.
- If the measured residual stress (rather than Equations (1a) and (1b) is used in the calculation of Kr in accordance with the R6 method, the analysis points for ‘high Lr’ specimens lie well above those generated using the BS 7910 method.
The intention of the work carried out by Formby 6 was to generate two sets of test data that were alike in every respect except for the presence of a residual stress field. The analysis points for the as-received specimens lie clustered around the FAL. Consequently, if the treatment of specimens containing residual stress is correct, the analysis points for the nine internally stressed specimens should also be clustered around the FAL. The specimens analysed using the BS 7910 method show points just outside and on the FAL, one on it and one inside it, so the treatment of specimens containing residual stress is seen to be very similar to that of as-received specimens.
Leggatt’s analysis of the specimens subjected to residual stress used the value of fracture toughness corrected for WPS effects as described by Formby and Griffiths 7, eg 68.8MPa√m instead of 26MPa√m at -196°C. Had the data for ‘virgin’ material been used instead, values of Kr would have been much higher.
It should be noted that, according to BS 7910, the starting point for all the tests containing a residual stress field is that of a uniform tensile residual stress, the magnitude of which is the room temperature yield strength, σ'YRT, of the material. This residual stress can be reduced to the value given by Equation (1b) if the output of (1b) is lower than σ'Y. The logic of this is that Equations (1a) and (1b) are applied only in cases where the user does not know what the actual residual stress distribution is. It can be argued, however, that if Equations (1a) and (1b) correctly describes ‘global’ residual stress relaxation, then they could be re-written with the known (measured) residual stress as the starting point as follows:
Qm is the lower of either
where σRM is the measured residual stress and σ’Y is the yield strength of the material at the assessment temperature.
In order to test the stress relaxation equations themselves, the CEGB specimens containing residual stress were re‑analysed using this fourth method, termed the ‘hybrid’ method, since it combines a starting assumption identical to that used in the R6 method, but assumes stress relaxation to occur in accordance with the principles of BS 7910. This approach is not mentioned in PD 6493 or BS 7910, although Leggatt4 hints that it should apply, thus: ‘In cases where the distribution of residual stresses is known, then a reduced level of residual stress may be assumed to be acting in the structure under load, as given by the following formulae:’. This was followed by the equivalents of Equations (2a) and (2b).
In the case of the CEGB specimens containing a residual stress field, four of the specimens were tested at low temperatures (three off at -196°C and one at -185°C). For these specimens, the value of Lr at failure is low, whilst σ’f and σ’Y have relatively high values. Consequently, the output of Equation (2b) is higher than that of (2a) and Qm=σRM. The analysis of these specimens is therefore exactly the same as the ‘R6’ analysis and has not been repeated.
The remaining five specimens were tested at a range of temperatures: -161, -126, -73°C and ambient temperature (two off), providing a realistic test of the validity of Equation (2b). Results of the ‘hybrid’ calculations for these specimens are the same as for the BS 7910 analysis. Leggatt’s equations thus appear adequate to handle residual stress distributions that are assumed to start at sub-yield values and to relax in accordance with the current BS 7910 clauses.
2.3 TWI wide plate tests
Figure 1 also shows the results of five parent material wide plate tests carried out by TWI as part of a European collaborative research project (indicated by five solid black circles at Lr values of around 1.0, enclosed in an ellipse marked ‘TWI plain WP’). The material used in this work was a well-characterised structural steel tested at -65°C, in the transition region. A ‘best estimate’ of fracture toughness, ie a mean rather than a lower bound value, was used in this analysis, with the result that the five analysis points straddle the Failure Assessment Line, with two in the ‘safe’ region, two in the ‘unsafe’ and one almost exactly on the line (see Figure 1). If the FAL provides a good description of the interaction between plasticity and fracture, this behaviour is to be expected, given that the tests were carried out on well-characterised parent material, using a simple geometry and with accurate laboratory measurement of failure conditions.
Results of a single ‘ring-welded’ wide plate test carried out by TWI on the same material at the same temperature are also shown in Figure 1 (red square at Lr~0.55). The analysis point lies inside the FAL when ‘best estimates’ of residual stress (ie as measured) and fracture toughness (median value) are used.
Results of these six tests (the five parent material tests and the ring-welded test) were reanalysed using BS 7910:2013 procedures, implemented via CrackWISE® software. Results are shown in Figure 4, with the test data plotted against both an Option 1 FAD (assuming discontinuous yielding) and an Option 2 FAD, which provides a more accurate description of the yielding behaviour of the material. From Figure 4, it is apparent that:
- The analysis of parent material specimens as described by Leggatt has been reproduced using BS 7910:2013.
- Leggatt’s analysis of the ring-welded specimen lies at Lr~0.55. The square red datapoint shown at Kr~0.82 in Figure 4 can be reproduced only if the measured value of residual stress (Qm=186N/mm2) is used. This would seem to comply with the recommended R6 method rather than the BS 7910 method, even though his paper states that assessments were made “…at Levels 1, 2 and 3 of the proposed new PD 6493 procedures…”.
- If the BS 7910 procedure is followed instead, with σ’YRT=355N/mm2 and residual stress relaxation is permitted as per Equations (1a) and (1b), Kr rises to 1.2 and the analysis point lies outside the FAD, ie the analysis is conservative, and (because Lr is too low to trigger global residual stress relaxation), Kr is higher than for the method based on the ‘as-measured’ residual stress.
- It appears that the square purple point at Lr~0.55, Kr~1.1 in Figure 1 represents an analysis of the ring-welded wide plate test using the ‘provisional’ PD 6493 residual stress relaxation equation as originally proposed by Garwood et al, which has, of course, now been superseded (see the companion paper1).
For the case of the single ring-welded specimen, the ‘R6’ analysis point lies inside the FAL, whereas the ‘BS 7910’ analysis point lies outside. Had several tests of this sort been carried out, using mean estimates of materials properties, the expectation would be that approximately half would lie outside the FAL and half inside, by analogy with the parent material results. All that can be stated at this stage is that the ‘BS 7910’ approach gives more conservative results, ie a higher value of Kr.
2.4 Validation against numerical analysis
Leggatt’s 1988 paper also cites a numerical analysis carried out by Hellen and Blackburn 13 and included in the validation document for R6 Rev 3 14. The analysis concerns a 20% centre-cracked plate made from a material with a high work-hardening capacity, eg an austenitic stainless steel. An elastic-plastic analysis of the plate under primary (tensile) and secondary (thermal) loading was made, and values of J‑integral for the various loading sequences are reported. Leggatt represented these analyses in the form of an FAD, comparing (in current R6 terminology) the Option 1 and Option 3 FADs. He identified the case σR=0.5σY as having the smallest inherent safety factor, ie this was the case at which the Option 1 and Option 3 curves were closest together. He confirmed the necessity for adding the ρ factor in order to ensure that the Option 3 curve was always outside the Option 1 curve (but also suggested applying a simple safety factor on Kr instead – a suggestion that was not subsequently adopted by BSI). He also showed the consequences of applying the stress reduction factor, based on the case σR=0.94σY, this being the highest level of residual stress considered by Hellen and Blackburn and the case for which residual stress reduction would be the greatest. The consequences of adopting Equations (1a) and (1b) were illustrated, and it was shown that their use was ‘safe’, ie (in R6 terms) the Option 3 FAD lay outside the Option 1 FAD.
Leggatt’s original work 5 can be reviewed to understand his analysis methods in more detail (the 1988 paper 4 does not contain sufficient detail to reproduce his analysis), as shown below.
The Blackburn and Hellen results were published by them in internal CEGB reports and in the International Journal of Fracture 13. Leggatt, however, did not use these FEA results directly. Instead, he used the presentation made by Milne et al 14 where the crack tip loading was converted into values of Kr and Lr together with a reported value of χ (Figure 5), where χ is given by the following expression.
where 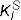 is the elastic value of Stress Intensity Factor (SIF) from secondary stresses alone and
is the elastic value of Stress Intensity Factor (SIF) from secondary stresses alone and 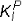
is the SIF due to primary stresses alone.
Leggatt assumed that the SIF coefficient for both 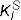 and
and 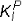 was the same for the primary stresses ( P M) and secondary stresses (Q). This meant that he could re-express Equation (3) as follows.
was the same for the primary stresses ( P M) and secondary stresses (Q). This meant that he could re-express Equation (3) as follows.
This expression was further reduced by the following expression.
Equations (4) and (5) provide the following two expressions.
Leggatt adopted the following expression for the residual stress remaining after the application of primary stresses.
The reduced level of residual stress could then be used to determine a revised value of χ as follows.
Expression (9) allows a new value of ρ to be calculated using the Ainsworth simplified equations, but based upon a reduced level of residual stress. The revised value was denoted ρ1.
Leggatt assumed that the original value of K r (Equation (10) below) would be reduced to a revised value, 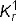 (Equation (11)).
(Equation (11)).
Kmat was assumed to be the same in both equations so:
Leggatt was therefore able to calculate 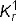 using Equations (6), (7) and(8) with Equation (14) for F and then Equation (12) with the previously evaluated ρ1.
using Equations (6), (7) and(8) with Equation (14) for F and then Equation (12) with the previously evaluated ρ1.
Leggatt analysed the curve presented by Milne et al (1987) that had the highest value of χ (equal to 1.17, see Figure 5). He digitised the points and used the approach described above to determine the coordinates (
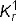
, L
r). The original and revised coordinates are presented in Figure 6 together with the two FADs. One FAD was presented in Milne et al (1988) and is shown as Equation (15) below.
The other FAD is the slightly revised version that is presented as Option 1 in R6 revision 4.
The results demonstrate that the residual stress reduction under primary loading proposed by Leggatt is less conservative than the original R6 approach proposed by Milne14 but is still conservative when compared to the two FADs.
3. Discussion
‘Validation’ (defined here as analysing actual experimental data in terms of an assessment procedure) can only ever show that a procedure is wrong (eg a point corresponding to failure lies inside the FAD), not that it is correct. There are multiple factors (in addition to residual stress) affecting the analysis: the particular SIF and reference stress solution adopted, the treatment of fracture toughness and tensile data and the treatment of stress concentrations to name just a few. The analysis carried out by Leggatt in support of the PD 6493:1991 procedure was designed to show the effects of altering just one variable, in this case residual stress. In the CEGB experiments, the material, and the flaw type, size and location were kept constant, and the use of a simple geometry allowed unambiguous definition of parameters such as SIF and reference stress. The only variables were temperature and residual stress, with pairs of specimens tested with and without a residual stress field to provide a critical analysis of the role of residual stress over a range of temperatures. In the TWI tests, a known material (in the form of centre-cracked plates) was tested to failure with and without the presence of a residual stress field. The crack lengths of the plates varied, and all were tested at -65°C, a temperature corresponding to the transition range for this steel. The presence of residual stress resulted in a marked reduction in failure stress. All results were analysed using at least two variants of the treatment recommended by BS 7910:2013:
- Assessment based directly on the experimentally-determined value of secondary stress (‘R6 method’).
- Assessment based on assuming yield magnitude residual stress, then allowing relaxation of residual stresses as per Equations (1a) and (1b) (the ‘BS 7910 method’).
An additional set of analyses was carried out using the so-called ‘hybrid’ approach, in which the initial value of measured residual stress, σRM, is used as the starting value, and relaxation of residual stress assumed to occur in accordance with the BS 7910 method. This method produces results equivalent to either the R6 method or the BS 7910 method.
The full analysis carried out by Leggatt has not hitherto been published in full. However, from an examination of the original work and a re-analysis in terms of BS 7910:2013, there is no suggestion that the method is unsafe. There are several minor anomalies in the way the work has been interpreted in successive versions of PD 6493 and BS 7910. For example, eg the definition of flow strength has changed over time from one based on 1.2σY to a value (σY+σUTS)/2, and it is not always clear from previous editions of PD 6493 and BS 7910 whether the tensile properties referred to are those at ambient temperature or at assessment temperature (which in turn could be either above or below ambient temperature).
Although the current study has not revealed any problems with the BS 7910 approach to residual stress relaxation, it should be noted that the ‘structures’ examined in this work are all very simple, ie uniaxially loaded centre-cracked sheets and plates. It is therefore considered prudent to re-examine some of the data and analyses produced after the publication of the 1991 version of PD 6493:1991, in particular those that involve biaxial loading and/or complex stress distributions. Where possible, these should be analysed/re-analysed in terms of the plasticity interaction factor V (as well as ρ), given that from 2013 onwards a V-based approach will be common to R6 and BS 7910.
4. Conclusions
- The residual stress relaxation clauses of BS 7910:2013 date back to the 1991 edition of PD 6493 and have not changed substantially since then.
- A considerable programme of work was carried out by TWI at the time to justify and validate the clauses, using a range of experimental and numerical work. This included analysis of work carried out by the CEGB (a forerunner of EDF Energy) and used by them in the validation of the R6 procedure. The full underlying details of the work have not hitherto been available in the public domain; a key report written by Leggatt in 1987 was never published outside TWI (although the conclusions arising from it were published in 1988). It is believed that this is the reason that R6 describes the work as having ‘limited validation’. The approach proposed in BS 7910 combines ‘global’ relaxation of residual stress (Qm) under high mechanical load with ‘local’ enhancement of crack tip driving force through the adoption of a simplified primary/secondary stress interaction factor, ρ. This is different from the method adopted by R6, but seems to be equivalent to allowing negative values of ρ under conditions of high primary stress.
- A re-analysis of Leggatt’s work, using the BS 7910:2013 clauses, has shown nothing to contradict the approach. Whilst there are minor anomalies in the way it is presented, and it is arguably counter-intuitive to have one term (r) increasing crack tip driving force and another (Qm) reducing it, the current approach represents a workable engineering solution to the problem of how to analyse residual stress effects in as-welded structures rapidly and reasonably realistically, and could reasonably be included in future amendments to R6.
- According to the current BS 7910 approach, residual stresses can be reduced by mechanical loading only if they are initially assumed to have yield strength magnitude. It is not clear why this restriction was imposed, but additional calculations based on assuming the measured value of residual stress as the starting condition, then allowing stress relaxation in a manner analogous to that described in BS 7910, do not alter the conclusions given above. This so-called ‘hybrid’ treatment of the data represents a realistic generalisation of the Leggatt method that would permit a more accurate assessment of structures/test specimens in which the original stress distribution is known to be sub-yield.
References
- PVP2014-28152, Effects of Mechanical Loading on Residual Stress and Fracture: Development of the BS 7910:2013 Rules, Isabel Hadley and Simon D Smith.
- BS 7910:2013 - Guide to methods for assessing the acceptability of flaws in metallic structures.
- R6 - Assessment of the integrity of structures containing defects, Revision 4.
- Leggatt R H (1988): ‘Investigation of proposed procedures for the inclusion of residual stresses in the revised fracture sections of PD 6493’, Proceedings of the international conference on Residual Stresses (ICRS2), Nancy, November 23-25, 1988.
- Leggatt R H (1987): ‘Investigation of proposed procedures for the inclusion of residual stresses in the revised fracture sections of PD 6493’, TWI report 7011/01.87/584.2.
- Formby C L (1980): ‘Compatibility of the CEGB procedure for assessment of the integrity of structures (R6) with experimental findings in the presence of residual stress’, Report NW/SSD/RN/116/79.
- Formby and Griffiths (1977): Formby C L and Griffiths J R, ‘The role of residual stress in the fracture of steel’, Conference on Residual Stresses in Welded Construction and their Effects, The Welding Institute, London, 1977.
- I Hadley and HG Pisarski: ‘Overview of BS 7910:2013’, FESI ESIA12 - 12th International Conference on Engineering Structural Integrity Assessment, 28-29 May 2013, Manchester, UK.
- Isabel Hadley: PVP2011-57307, ‘Progress towards the revision of BS 7910’, Proceedings of the PVP2011 Pressure Vessels and Piping Division Conference, 17-21 July 2011, Baltimore, Maryland, USA.
- Isabel Hadley, Bob Ainsworth, Peter Budden, John Sharples: PVP2010-25582, ‘The Future of the BS 7910 Flaw Assessment Procedures’, Proceedings of the ASME 2010 Pressure Vessels and Piping Division Conference, (PVP2010), July 18-22, 2010, Bellevue, WA, USA.
- Sharples et al (2011): Sharples J, Gill P, Wei L and Bate S, ‘Revised Guidance on Residual Stresses in BS 7910’, Proceedings of the ASME 2011 Pressure Vessels & Piping Division Conference (PVP2011), July 17 - 21, 2011, Baltimore, Maryland, USA. Paper No. PVP2011-57071.
- Ainsworth (1986): Ainsworth R A, ‘The treatment of thermal and residual stresses in fracture assessments’, Engineering Fracture Mechanics 24 1 65-76.
- Hellen and Blackburn (1986): Hellen T K and Blackburn W S, ‘Post-yield fracture mechanics analysis of the combined thermal and mechanical loading of a centre-cracked plate’, International Journal of Fracture, 32, 185-199 (based on TPRD/B/0613/R85, 1985).
- Milne et al (1988): Milne I, Ainsworth R A, Dowling A R and Stewart A T, ‘Background to and validation of CEGB report R/H/R6 – Revision 3’, International Journal of Pressure Vessels and Piping, 32, 105-196.
Figure 1 Extract from Leggatt’s 1988 publication4,
showing FAD-based analysis of wide plate test data.
Figure 2 BS 7910:2013 Option 1 FAD, showing analysis of CEGB
test data for as-received wide plate specimens.
Figure 3 FAD showing analysis of CEGB test data
for wide plate specimens containing residual stress.
Figure 4 FAD showing analysis of TWI wide plate
test data in accordance with BS 7910:2013 rules
Figure 5 Leggatt5 copy of Figure 17 from Milne et al14.
Figure 6 Comparison of the original data points (Kr, Lr)
presented by Milne et al14 with the revised data points
(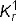 , Lr) computed by Leggatt5 based upon his formula
, Lr) computed by Leggatt5 based upon his formula
for residual stress reduction under the action
of primary loads.