Creep Crack Growth Prediction of Very Long Term P91 Steel Using Extrapolated Short-Term Uniaxial Creep Data
S. Maleki
TWI Ltd
A. Mehmanparast, K. M. Nikbin
Imperial College London
Paper presented at the 2013 ASME Pressure Vessels and Piping Conference. Paris, France, 14-18 July 2013.
ABSTRACT
Practical time frames in newly developed steels, and technical and financial restrictions in test durations means that extrapolation of short-term laboratory test results to predict long-term high temperature service component failure is an area of concern when conducting a fitness for service or remaining life assessment. Recent literature presenting uniaxial creep and crack growth tests indicate that some materials show lower failure strains during longer term laboratory tests. The constraint based remaining failure ductility based NSW model crack prediction model has been shown to be capable of predicting upper/lower bounds of creep crack growth in a range of steels when data are obtained from relatively short to medium-term laboratory experiments ( < 10,000 hours). This paper compares and analyses the response of the NSW model to predict long term creep crack propagation rates using a wide database of modified 9Cr material over s range of temperatures. The paper employs extrapolation methods of available uniaxial data to make viable conservative predictions of crack growth at high temperatures where at present no data is available.
Nomenclature
| θ |
The crack tip angle |
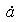 NSW NSW |
NSW creep crack growth rate |
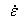 |
Steady state creep strain rate |
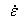 A A |
Average creep strain rate |
| εf |
Uniaxial creep failure strain (creep ductility) |
| ε* f |
Multiaxial creep ductility |
| A |
Power law coefficient in steady state creep strain rate law |
| AA |
Power law coefficient in average creep strain rate law |
| n |
Power law exponent in steady state creep strain rate law |
| nA |
Power law exponent in average creep strain rate law |
| C* |
Steady state creep fracture mechanics parameter |
da/dt,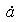 |
Creep crack growth rate |
| In |
The non-dimensional function of n in NSW model |
| rc |
Creep process zone |
| σ |
Applied stress |
| Br |
Power law coefficient in rupture time creep law |
| tr |
Rupture time |
| νr |
Power law exponent in rupture time creep law |
| D |
Power law coefficient in empirical creep crack growth law |
| ϕ |
Power law exponent in empirical creep crack growth law |
| r |
radial distance ahead of the crack tip |
Introduction
The nominal design life for power plants is generally 100,000 hours. However, in most cases the actual service life of pressure components is considerably more than this limit. Also long term high temperature uniaxial data is not practically available for assessing design life in high temperature applications for newly developed alloys such as P91. This may imply that the data, assumptions and safety factors applied in the design and life assessment stage need to be over conservative. Looking at the current service life of most power plants indicates that the above assumption is correct as the majority of their equipment have been operating for more than 100,000 hours.
When a defect (i.e. a crack like flaw) is present in a component, assessment of fatigue, creep or creep-fatigue to predict the remaining life requires laboratory test data. This remaining life evaluation needs a higher level of accuracy compared to the design stage as a pessimistic analysis may lead to an unnecessary interruption in plant operation. On the other hand, an underestimation may result in a catastrophic failure which will be followed by safety and business consequences. This type of assessment usually relies on laboratory test data which is generally collected in an accelerated damage propagating condition by increasing key test parameters such as stress or temperature to a higher value than actual service condition and then extrapolating the results to the service condition. This paper aims to evaluate the effect of this extrapolation in Creep Crack Growth (CCG) predictive models by using the short-term and long-term laboratory test data.
Predictive model for steady-state creep crack growth
At an elevated temperature, metals may exhibit a stress dependent deformation rate. This deformation is usually composed of three regions known as primary, secondary (or steady-state) and tertiary. In practical applications, in service at load and temperature, the steady-state region usually dominates the life of the component subjected to creep deformation. In the steady state condition, this high temperature creep deformation rate, , may be related to the stress by a power law;
where A and n are the steady state power law creep stress coefficient and exponent, respectively. If particular values of A and n for steady-state condition are not available, it is possible to use the average values in equation 1 and express the strain rate as an average value,
When a cracked body operates at an elevated temperature where creep is the dominant failure mechanism, a time dependant crack growth is observed. The relationship for crack growth rate under steady-state creep dominant conditions in engineering alloys has been shown to be represented by the power law relation [1]:
where C* is the steady state creep fracture mechanics parameter and D and ϕ are the creep crack growth (CCG) power law coefficient and exponent, respectively.
For a power law creeping material which follows Eq. (1), the steady crack tip strain rate can be expressed by [1]:
is the normalising strain rate, σ0 is the normalising stress, r is the radial distance ahead of the crack tip, In is a non-dimensional function of n, and
is an angular function of the crack tip angle, θ, and n. Nikbin et al [2] illustrate in predictive models of the CCG process that creep crack growth rate is inversely proportional to the creep ductility of the material. The model is referred as the NSW model (after Nikbin, Smith and Webster). This model assumes that failure occurs at crack tip when the available material creep ductility is exhausted and
reaches its maximum value of unity and gives the following expression for the creep crack growth rate [1];
where rc is the creep process zone (which is often taken as the average grain size of the material) and ε* f is the multiaxial creep ductility (appropriate to the state of stress at the crack tip). It is recommended in [3] that for most relevant engineering materials, the creep ductility ratio between the extreme multiaxial, plain strain, and uniaxial, plain stress conditions to be taken as 1/30. Comparison of the CCG rate for creep ductile material shows the maximum value of CCG rate under plane strain conditions is about 3 to 7 times greater than that under plane stress, although the ratio depends on the value of n [4].
Using the failure strain criteria, the CCG rate can also be predicted by rupture data. The average creep rate,
which account for all three creep regions can be defined as:
where εf is the uniaxial creep strain at failure (creep ductility), tr is the time to rupture, and AA and nA are the average creep strain rate power law coefficient and exponent, respectively. The rupture life can also be related to the stress using a power law relation as:
where Br and vr are the rupture time power law coefficient and exponent, respectively. By combining Eq. (5) and (6), the creep ductility can be estimated by:
Based on Eq. (7) if nA = νr then the creep failure strain is independent of stress. When nA > νr creep ductility decreases with decreasing stress. CCG can be predicted by combining the above equation with the failure strain criterion. There are a number of factors affecting this estimation such as the formula adopted for assessment [5], test condition [6], laboratory specimen geometry/size and creep ductility. The difference between plane stress and plane strain CCG based on the NSW model for the creep ductile material was very large, a factor of about 30. However this is reduced to a factor of approximately 6-7 for n values between 7-10 when the modified version of the NSW model was used [7].
Long-term ccg rate prediction based on uniaxial data
The modified 9Cr base (parent) material, as a creep enhanced ferritic steel, were selected for this study due to the current industrial concern of long-term aging problem associated with this material [8]. Data have been provided by Imperial College London, TWI, ANSTO and National Institute for Material Science [9-10] for a range of test durations from a few hundred hours in high stress (i.e. short term) tests to almost 70,000 hours in low stress (i.e. long term) range close to service stresses. The following analysis aims to predict the creep crack propagation behaviour of this type of steel material for long-term crack growth performance using lower bound creep properties and failure strain which are likely to occur in extremely long term tests. For modified 9Cr material, all analyses were focused on the data collected at 600 oC (and to lesser extend at 625 oC) as this is the temperature the steel is most likely to operate at in power plants.
Figure 1 shows the plot for Eq. (5) in the logarithmic scale for the modified 9Cr steel parent material. Note that the data provided in this figure have been obtained from different batches of materials subjected to different heat treatments prior to testing and are therefore likely to show increased scatter. However, they have been considered as a single set of data to deduce the creep strain rate trends in the inherent creep data scatter. In this figure the applied stress is normalised by the proof stress to illustrate the level of plasticity. The proof stress used here 394 MPa at 500 oC, 349 MPa at 550 oC, 272 MPa at 600 oC and 183 MPa at 650 oC. However, as it is shown in Figure 1 the contribution of plasticity in the creep deformation behaviour of the material is negligible at the examined temperatures. As shown in Figure 1, a change in the average creep strain rate exponent, nA , can be observed from short term to long term test data at the range of temperatures examined. Also shown in this figure is that a trend (shown by a dashed line) between the normalised stresses at which the transition from short term to long term creep strain rate slopes and the temperature may be inferred. This is simplified by determining a transition point to indicate a lower/upper bounds for long and short term test times. Table 1 shows the σ/σ0.2 values at the transition points for different temperatures.
The best average of individual slopes at each temperature has been fitted to the data using the least squares method in Figure 1. The same behaviour has also been observed in C-Mn steel [11]. There are at present little or limited long term creep data that can be found in the literature for modified 9Cr. This is partly due to the relatively recent development of the alloy and partly due to data not being in the public domain. Either way for the purpose of this analysis an assumption of a transition point is conservative in terms of life assessment at long terms. In this analysis the values of nA = 13 and nA = 5 have been used for the modified 9Cr base metal at 600 °C in short-term and long-term estimations, respectively, considering the transition points indicated in Table 1. The same slopes have also been employed to provide the line of best fit at other temperatures even where limited data are available.
As seen in Eq. (4), the most sensitive parameter in the NSW prediction model is the creep ductility. Figure 2 gives the plots for modified 9Cr based metal creep failure strain versus the applied stress normalised by the proof stress of the material at each temperature. Figure 2 shows that a strong stress dependency may be inferred in the creep ductility of the material at different temperatures. Although data show a large scatter, a drop in failure strain is apparent when the applied stress decreases, especially in the higher temperature range. This means the material should satisfy the condition of Eq. (7) and shows nA > νr (note that for brevity, the rupture time data are not shown here, however the data at 600 °C confirm that nA > νr ). The stronger dependency of failure strain on applied stress at higher temperatures could be due to the effect of aging which is accelerated at higher temperatures.
If it is assumed the tensile test results at any temperature represent the highest level plasticity, this could be aligned with the upper-bound for creep ductility. Figure 2, shows this assumption can be considered valid for uniaxial creep test, especially at higher temperatures. The upper-bound value of tensile strain at failure for each temperature is provided in table 1. For the lower bound failure strain, an initial assessment would be the failure strain at the transition points identified in Figure 1 and listed in Table 1. Using the same σ/σ0.2 values for the failure strain it is clear that there is very little data available for all the temperatures to determine a transition lower-bound. It is likely that P91 does not exhibit a very sharp change in failure strain with respect to stress at longer times. The average of individual slopes has been worked out and fitted to the data, using least squares method, for the range of temperatures examined in figure 2. It is also clear that there is no lower-shelf behaviour apparent in this data set. This could be because there is no longer term data available or possibly due the inherent brittle nature of P91 which fails at very low σ/σ0.2 values of between 0.3-0.6 σ/σ0.2 over the whole of the stress range observed.
In addition the definition of creep ductility or failure strain may vary based on the material. In a general approach, failure strain is assumed to be the strain at the time of failure. However, a closer look at most of the creep curves, indicates that a big increase in strain to failure takes place toward the end of the life. This can be due to a considerable amount of necking which happens at the end of the life in a test specimen and possibly thin wall tubes in practice. On the other hand, once the material enters the tertiary creep region, it is not considered to be fit for service anymore. This is generally the case for P91 steel as shown in Figure 3. Therefore an alternative definition of failure strain could be adopted using the strain at the end of secondary (steady-state) region. Figure 3 illustrates these two definitions. This approach known as Monkman-Grant Ductility (MGD) has been used for P91 Parent material previously [12]. Using this method, MGD at various ranges of temperature and stress is presented in figure 4. The immediate conclusion from this figure is that the graphs in figure 4 present marginally less scatter compared with figure 2 and also there is more apparent dependency of MGD to stress. The comparison between the failure strains at different stresses still satisfies the power law relationship between creep ductility and applied stress. This method is expected to be a better and more conservative assessment of failure strain for longer term component behaviour
To apply the above discussion to the predictive CCG models, P91 scatter band developed in the previous work [7] was used together with recent test data developed at Imperial College London and TWI Ltd together with data from [3]. Figure 5 summarises the results. Here, an overall value for high stress and low stress condition from figure 1 (nA = 9.7 and AA = 2 x 10-26 ) were assumed to fit in Eq. (1). For NSW plane stress condition, the creep ductility was assumed to be the failure strain at the tensile. Using a constant value from the tensile failure strain data (εf = 33%) in NSW model provides Eq. (2) as follows:
The plot of this equation is given in figure 5. Comparing this plot with P91 scatter band [7] shows it fits well with the lower band for the current available CCG data in high value of C* and consequently in lower C* values. It should be noted that this is considered to be in plane stress condition therefore higher predictive values of CCG rate are expected when considering a plane strain condition. For NSW plane strain condition, the creep ductility was assumed to be the lower creep ductility observed in figure 2, as assumed to be the lower bound ductility limit.
Using a constant value from the failure strain data at the transition point from figure 2 (εf = 18%) in NSW model provides Eq. (2) as follows:
The prediction is closer to the middle of the data band. However it is still unable to provide a conservative prediction of the upper band. To fix this problem, another approach was adopted where the creep ductility is assumed to be obtained from the MGD approach (see figure 3). The failure strain obtained from this approach at transition point (εf = 0.8%) was used in NSW model which will provide Eq. (2) as follows:
The plot of this equation in Figure 5 shows it can appropriately predict the upper bound CCG rate from existing test results.
To illustrate the most extreme case, the lowest MGD from figure 4 (εf = 0.2%) was also used. This value may be obtained by applying the method from figure 3 to longer test duration; if the criteria of the failure strain is considered as the cross section of secondary creep and rupture time, a value of 0.2% creep ductility could be assumed for long-term uniaxial test which corresponds to low C* creep crack growth experiments. In the previous work [7] it was shown that current scatter band is only validated for values of C* greater than 10-6 MPam/h. From figure 5, the following equation is proposed for CCG rate prediction for P91 when C* < 10-5MPam/h gives:
As seen in Figure 5, this approach provides the prediction line which is more likely to be capable of predicting the long-term CCG behaviour of modified 9Cr based material. The validation of this analysis is crucial and long-term CCG data are needed to support the prediction model.
Despite fact that the long-term CCG data are not available for this material, long term CCG tests on grade 316 stainless steel by EDF Energy Ltd [13] indicate that the correlations show similar trends to the prediction shown here for P91.
Conclusions
A detailed study of uniaxial creep data from a wide range of stresses for modified 9Cr material steel over a range of temperatures indicates a change in the creep exponent and failure strain at longer creep times. The failure strain also tends to decrease with a decrease in the applied stress. It is found that the appropriate failure strain under multiaxial stress state can be estimated by extrapolating secondary strain (Monkman-Grant Ductility) to the failure time rather than the final failure strain (which is attained at the end of tertiary region).
Using the extrapolated uniaxial failure strain data at the lower shelf (low stress) region and a reduced creep index at long terms, conservative CCG predictions have been made by the NSW model. For C* values of 10-5 MPam/h and less, cracking is predicted to be relatively faster compared to the extrapolated short term CCG data trend. It is important to note that the assumption of lower failure strains and reduced creep indices will effectively produce a safe prediction for CCG using the NSW model. However the level of conservatism increases depending on the use of uniaxial failure strains or the Monkman grant failure strain or in the extreme 0.2% failure strain as the lower shelf data. The correct level of conservatism can only be determined once actual long term data are available.
Acknowledgements
Thanks to Dr. Masaaki Tabuchi of NIMS, Dr. Masataka Yatomi of IHI, Warwick Payten of ANSTO and other researchers at TWI and Imperial College London for assistance and providing data for this project.
References
- Webster G A and Ainsworth R A. High temperature component life assessment. London. Chapman & Hall: 1994.
- Nikbin K M, Smith D J and Webster G.A. An engineering approach to the prediction of creep crack growth. J. Eng. Mat. And Tech. ASME 108, 1986, p.186-191.
- Tan, M , Celard N J C , Nikbin, K M and Webster, G A. Comparison of creep crack initiation and growth in four steels tested in HIDA”, Int. J. Pres. Vessel and Piping. 2001; 78, p.737–747.
- Yatomi M, O’Dowd N P, Nikbin K M and Webster G A. Theoretical and numerical modelling of creep crack growth in a carbon-manganese steel. In: Journal of Engineering Fracture Mechanics 73, 2006. p. 1158–75.
- Wasmer K. Nikbin KM. Webster GA. A sensitivity study of creep crack growth in pipes. ASME PVP. HighTtemp. of Structures and Materials. Vol. 438, p.17 24.
- Nikbin K M. Creep and creep/fatigue crack growth modelling and testing methods relevant to life assessment of cracked component. Welding Research Council Bulletin 512: 2006.
- Maleki S, Zhang Y-H and Nikbin K. Prediction of creep crack growth properties of P91 parent and welded steel using remaining failure strain criteria. Journal of Engineering Fracture Mechanics Available online 24 April 2010.
- Abson D J and Rothwell J S. Review of Type IV Cracking in 9-12%Cr Creep-Resistant Martensitic Steels. TWI, Granta Park, Great Abington, Cambridgeshire, CB21 6AL, UK.
- NIMS creep data sheet. Atlas of creep deformation property No. D-1. Creep deformation properties of 9Cr-1Mo-V-Nb steel tubes for boiler and heat exchanger. National Institute for Material Science, Japan 2007.
- NIMS creep data sheet. Atlas of creep deformation property No. D-1. Creep deformation properties of 9Cr-1Mo-V-Nb steel plate for boiler and heat exchanger. National Institute for Material Science, Japan 2007.
- Masataka Yatomi. Factors affecting cracked component at elevated temperature. A thesis submitted for the degree of doctor of philosophy of University of London and Diploma of Imperial College. June 2003.
- B.K. Choudhary, E. Isaac Samuel. Creep behaviour of modified 9Cr–1Mo ferritic steel. Journal of Nuclear Materials 412 (2011) 82–89
- Dean D W and Gladwin D N. Creep crack growth behaviour of Type 316H steels and proposed modifications to standard testing and analysis methods. International Journal of Pressure Vessels and Piping 84 (2007) p. 378–395.14.
Tables
Table 1: Failure strains used in NSW predictions
| Test Temperature (oC) |
Tensile Strain at Failure (%) |
σ/σ0.2 at the transition point |
% creep ductility at the transition point (from figure 2) |
% creep ductility at the transition point (from figure 4) |
| 500 |
22 |
0.62 |
13 |
- |
| 550 |
27 |
0.52 |
15 |
0.6 |
| 600 |
33 |
0.46 |
18 |
0.8 |
| 650 |
38 |
0.43 |
22 |
1.2 |
Figures
Figure 1: Average creep strain rate versus normalised stress
Figure 2: Creep failure strain versus normalised applied stress
Figure 3: Comparison of failure strain determination methods (provided by National Institute for Material Science)
Figure 4: Monkman Grant creep failure strain versus normalised applied stress
Figure 5: Extrapolation of creep crack growth rates at the low C* regime compared with the short term scatter band of Modified 9Cr CCG data at 600 oC