Corrosion Damage Assessment and Burst Test Validation of 8in x 52 Linepipe
Annette D Karstensen and Alan T Smith
Structural Integrity Technology Group
TWI Ltd
Great Abington
Cambridge CB1 6AL
UK
Stuart N Smith
Amerada Hess Ltd
Scott House
Harness Road
Aberdeen AB1 4LE
UK
Paper presented at ASME 2001 Pressure Vessels and Piping Conference, Atlanta, Georgia, July 22-26 2001
Abstract
Severe corrosion pitting was found in an 11km long, multi-phase subsea flowline connecting a subsea manifold to a fixed platform in the North Sea. To determine the burst pressure as a function of the remaining ligament thickness, FE-Analyses were carried out on an 8in diameter linepipe with a nominal thickness of 14.3mm. The pits were approximately hemispherical of diameters 15 and 25mm, and the remaining ligament varied from 5 to 0.5mm. Because of the small ligament, FEA was used to predict the burst pressure of individual pits. To validate the FE-Analysis, a burst test was carried out on a piece of 8in diameter X52 linepipe with welded end caps. A simulated pit with a remaining ligament of 3mm was machined into the inside of the pipe wall, and the pipe was instrumented with strain gauges at 4 different positions. The pipe was pressurised using water until the burst pressure was reached. In addition an assessment of the corrosion was carried out using procedures suggested in BS7910 Annex G. The comparison of theory with experiment showed very satisfactory correlation, which will give added confidence in using the techniques in the future.
Introduction
Gas and oil pipelines can be affected by internal and external corrosion. The accurate assessment of corrosion damage is complex and requires a combination of inspection, corrosion, material and structural analyses. In a recent review of corrosion assessment methods for linepipe (
Smith, 2000), the preferred method for assessing single corrosion was that given in
BS7910 Annex G (1999). This method was less conservative than other assessment methods, but always resulted in safe predictions when compared with burst test results. Alternatively, finite element modelling techniques can be used to assess the integrity of the corroded pipe, however, this requires an accurate description of the corroded surface, and this can be time consuming to determine and is therefore not always practical. However this method gives accurate prediction of the burst pressure and is further considered in this paper.
Finite element analysis of 8in diameter linepipe with corroded pits
The maximum allowable pit size according to the assessment procedure given in BS7910:1999 Annex G is 85% of the wall thickness. The small remaining ligament heights in the corroded linepipe under consideration were beyond the validity limit of the assessment procedure and therefore finite element analysis was used to determine the integrity of a corroded linepipe as a function of pressure for a range of defect sizes. These analyses related the critical pressure condition to the remaining ligament thickness. An initial assumption was made that the corrosion could be represented by spherically shaped corrosion pits of diameter 25mm and 15mm.
Defect geometry
The various cases analysed are given in
Table 1. Five cases were completed for each pit diameter, and one additional analysis was carried out on the geometry identical to that used in the pressure test.
Table 1 Summary of corrosion cases analysed using FEA
| FE model | Spherical diameter
of defect,
mm | Thickness of
remaining ligament,
mm | Wall thickness,
mm | Outer diameter
mm |
|---|
| Case 15-5 |
15 |
5 |
14.3 |
219 |
| Case 15-3 |
15 |
3 |
| Case 15-1 |
15 |
1 |
| Case 15-0.75 |
15 |
0.75 |
| Case 15-0.5 |
15 |
0.5 |
| Case 25-5 |
25 |
5 |
14.3 |
219 |
| Case 25-3 |
25 |
3 |
| Case 25-1 |
25 |
1 |
| Case 25-0.75 |
25 |
0.75 |
| Case 25-0.5 |
25 |
0.5 |
| Pressure test |
21.7 |
3 |
13.9* |
219 |
Note:
* based on the average of five readings |
Modelling Parameters
The models were generated using the mesh pre-processor FAM supplied by FEGS Ltd while the analysis was carried out using the finite element code
ABAQUS Version 5.6 (1998).
The mesh was made using eight noded brick elements (ABAQUS type C3D8). Each model consisted of typically 2000 elements. Analyses were made allowing for large geometry changes by specifying the ABAQUS option NLGEOM in the analyses method, a typical mesh can be seen in Fig.1 where the full pipe is shown in its full length with applied symmetry boundary conditions together with a close-up of a corrosion pit.
It was assumed that the pipe is only subjected to internal pressure, this pressure was applied as a distributed loading on each internal element face. This pressure remains normal to the local surfaces, and is applied in typically 20 load steps, where the pressure increases for each load step.
Due to symmetry only quarter of the pipe was modelled, and symmetry boundary conditions were applied as appropriate.
Fig.1. Finite element mesh of 8in OD pipe, (Case 15-3) a) Mesh with applied symmetry boundary conditions
Material properties
It was assumed that brittle fracture was not of concern. This assumption is valid where the Charpy energy is above the accepted design requirement and no crack-like flaws are present in the structure. Sets of three Charpy specimens, aligned transverse and longitudinally to the pipe axis were taken from a representative section of 8in pipe. The specimens had a minimum Charpy impact energy of 292J at room temperature. While this toughness may be lower at normal operating temperatures (say 5°C), it can nevertheless be concluded that the risk of brittle fracture will be low.
For the finite element analyses, the material properties used were based on the minimum specified properties given for API 5L X52 line pipe ( see Table 2). The true stress-true strain curve was obtained by assuming linear elastic behaviour to yield, followed by a linear true stress-plastic strain curve between yield and the ultimate tensile stress. The maximum engineering stress was assumed to occur at 10% strain. This assumption is considered conservative.
Table 2 Summary of minimum material properties specified for API 5L X52
| Elasticity | Yield |
|---|
| E 1, MPa |
ν |
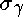 , MPa , MPa |
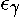 |
| 2.05x10 5 |
0.3 |
358 |
0.0017 |
| Failure |
|---|
σUTS,
MPa | 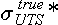 MPa MPa | 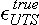 | 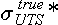 |
|---|
| 455 |
501 |
0.095 |
0.1 |
Note:
* assumed |
Limiting conditions
Burst condition
The criterion for failure as predicted by FE-analysis was based on a method suggested by
Fu and Kirkwood (1995b). This assumes that failure occurs by plastic collapse when the von Mises stress level at the external wall surface in the corroded pit reaches a true stress level of the material UTS. This proposed criterion incorporates both the material strength and the structural constraint.
Maximum allowable operating pressure condition
Data from Amerada Hess indicate that a design factor on hoop stress of 0.72 was used for the 8in production/test pipe. It was therefore decided to define the maximum allowable pressure when the membrane stress in the corroded ligament reached 0.72 specified minimum yield strength, (SMYS). This pressure is a limiting design pressure rather than a failure criterion.
Results and discussion of finite element analysis results
The predicted values of burst pressure and pressure at which the membrane stress in the remaining ligament reached 0.72 SMYS are given in
Table 3 and illustrated graphically as a function of remaining ligament thickness in
Fig.2.
Table 3 Summary of pressure at 0.72 SMYS
| | Pressure at 0.72
SMYS, bar | Burst pressure,
bar |
|---|
| C15-5 |
253 |
579 |
| C15-3 |
231 |
553 |
| C15-1 |
234 |
548 |
| C15-0.75 |
230 |
545 |
| C15-0.5 |
226 |
542 |
| C25-5 |
264 |
560 |
| C25-3 |
230 |
529 |
| C25-1 |
212 |
528 |
| C25-0.75 |
204 |
525 |
| C25-0.5 |
199 |
523 |
Comparison of the predicted critical pressures for 25mm diameter and 15mm diameter corrosion pits, shows that both the burst and 0.72 SMYS conditions are relatively insensitive to the assumed pit dimensions. This is in general agreement with other published results, ( Fu and Kirkwood, 1995a).
The figure shows that the 15mm diameter pit has a greater predicted burst pressure than the 25mm diameter defect. For the 0.72SMYS ligament stress the difference between pit sizes is small.
Fig.2 Pressure at 0.72SMYS and burst as a function of remaining ligament
Consideration of the results for burst and 0.72 SMYS criteria show that the limiting condition is relatively insensitive to the height of the remaining ligament for thicknesses exceeding 0.5mm. Although no FE analyses were performed for remaining ligaments less than 0.5mm thick, it can be presumed that there is a stronger dependence between ligament height and the limiting condition in this range. The reason for this is that although yielding in the remaining ligament will occur at a low pressure, this yielding is constrained by the surrounding (predominantly elastic) material and load is shed to this region. This prevents collapse of the ligament, and ensures that the failure pressure of the corroded pipe is close to that of the uncorroded pipe.
It should be noted that the actual failure pressure in the production/test pipe will be governed by the details of the pit configuration and may vary considerably from the predicted pressure for a smooth pit. In addition the predicted failure pressure will be non-conservative for corroded regions of greater axial or circumferential extent or where corrosion pits are grouped in closely spaced clusters.
Burst testing of simulated corrosion flaw
Introduction
A piece of 8in OD X52 linepipe was tested to determine the mechanical behaviour of the tube under hydrostatic burst test conditions. The information provided by this test was then examined to confirm the burst pressure predicted by finite element analysis. The FEA was performed on this pipe using data and geometry specific to the pipe. The procedure used is described in this section.
Burst Test Procedure
A 'corrosion' pit was manufactured by machining a spherical pit with a 24mm diameter on the inside surface with a ligament of nominally 3mm. The sample pipe was approximately 550mm long (see
Fig.3), ensuring minimal effects due to the presence of the end caps. To enable machining of the pit, a 'window' was cut in the pipe wall opposite the defect. After machining, the section of removed pipe was welded back into the pipe.
The burst test specimen was strain gauged using the arrangement shown in Fig.3. This consisted of two post yield biaxial strain gauges located at 3mm from the centre of the defect and aligned parallel to the axial and hoop directions. In addition, standard stacked biaxial strain gauges were remote to the pit to record the hoop and axial strains. All gauges were physically remote from the longitudinal and circumferential weld seams.
Fig.3. Burst test specimen
Strain, time and pressure were recorded and, in addition, the pipe was monitored using a remote video camera synchronised to the pressure display.
The pipe was pressurised using water at an initial rate of approximately 1 bar/second. After reaching 100 bar the pipe was depressurised. The pipe was then repressurised and the pressure was maintained at the following levels, 101, 128, 198, 286, 375, 405, 427, 451, 494, 522 and 550 bar. This was to monitor whether creep was taking place. Finally, the pipe was pressurised to the burst condition, which was also recorded by video.
Tensile tests
Full stress/strain curves were obtained as an average from six specimens for use in the finite element analysis, see
Fig.4, (three specimens were extracted from the circumferential direction and three from the axial direction of the pipe). A non-contacting extensometer using a high resolution CCD video camera with custom built software was used to determine the stress/strain curve. All tests were carried out at ambient temperature (approximately 20°C) under cross head displacement control at a displacement rate of 1mm/min. The output of each test consists of load, specimen elongation, minimum cross sectional diameter and crosshead displacement data. The average yield stress was measured to 430 N/mm
2 and the average UTS was measured as 530N/mm
2.
Fig.4. Material properties used in FE-analysis
Finite element analysis of burst test specimen
Parallel to the burst test programme, the specimen was analysed using finite element modelling techniques. The procedure for this is as described in Section 2, however, for this case the geometry used was that of the actual pipe and the mechanical properties were based on those of the burst test specimen.
End caps were incorporated into the mode of the burst pressure test. The mesh with the applied boundary conditions can be seen in Fig.5(a) and details of the pit are shown Fig.5(b).
Fig.5. Detail of FE-model for simulated burst test a) FE-mesh with applied boundary conditions
b) Detail of mesh around defect
Figure 6 shows the von Mises stress as a function of pressure for the inside surface, mid-thickness position of pit ligament and outside pipe surface at the pit position. Failure is predicted when the von Mises stress level at the external wall surface in the corroded pit reaches a true stress level at the materials UTS, this occurs at 680 bar.
Fig.6 FE prediction of burst condition for the pressure test
Results of pressure test
During pressurisation the pressure was increased in increments and held approximately constant for a period of time, until the strain was approximately constant. The graph of measured hoop and axial strain is compared with the hoop and axial strain predicted by FEA for this position in Fig.7. The predicted hoop and axial strain away from the pit is shown as a function of pressure in Fig.8 and these are compared to the measured hoop strain at this position. Unfortunately, the hoop gauge close to the pit location ceased working at a pressure of 572 bar and strain of 3.8%,(see Fig.7a).
Fig.7a) Comparison of measured hoop strain versus FE prediction 3mm from pit centre
Fig.7b) Comparison of measured axial strain with FE prediction 3 mm from pit centre
The general trend of the experimental data was for the hoop strain to linearly increase with pressure until the pressure reached approximately 450 bar (see Fig.7 and 8). At this pressure there was a sudden change in the experimental rate of hoop strain accumulation with respect to pressure. The experimental behaviour shows a similar trend to that predicted by FE analysis, however, the transition from low strain accumulation to high strain accumulation occurred at a higher pressure in the FE model (650 bar c.f. 450 bar). The burst condition was recorded visually using the remote video camera. This occurred at a pressure of 662 bar.
After testing the vessel was sectioned through the pit. A photograph of the section in the vicinity of the defect is shown in Fig.9. The section shows extensive neck formation prior to failure, with little evidence of any bulging effect taking place.
Fig.8a) Comparison of measured hoop strain versus FE prediction remote from the pit
Fig.8b) Comparison of measured axial strain with FE prediction remote from the pit
Fig.9 Section of machined 'corrosion pipe' after burst testing
Determination of failure pressure according to BS 7910:1999
The failure pressure was calculated according to BS7910:1999 Annex G, which gives guidance for assessing the pressurised pipes or vessels when loss of wall thickness is caused by either internal or external corrosion. The failure pressure (Pf) for a single flaw is calculated as:
P f = P o x R s
R s is the reserve strength factor which for this case was calculated as 0.92, which means that the pipe specimen was predicted to be capable of withstanding more than 90% of the failure pressure of an unflawed vessel.
The failure pressure in the vessel with no defect is determined as:
The relevant parameters and results are given in Table 4 below, the ultimate tensile strength was obtained from the tensile test as described above.
Table 4 Summary of input data for BS7910 assessment
| B o, mm | σ u, N/mm 2 | D, mm |
|---|
| 13.9 |
530 |
219 |
| R s | P o, bar | P f, bar |
|---|
| 0.92 |
718 |
661 |
Discussion
The tensile tests showed very similar behaviour for both the circumferential and longitudinal specimens. The results from the tensile test show that the assumed true stress-true strain curve based on specified minimum values of tensile and yield strength are conservative within the strain regime used in the FE analysis (i.e. up to 9% strain) (see
Fig.4).
Room temperature creep was observed to occur when the pipe was pressurised to above 375 bar and held at that pressure. No creep was observed at a pressure of 286 bar, but the holding time was relatively short. Some degree of creep could be expected to occur between 286 bar and 375 bar. However, it is not possible to determine precisely the threshold at which creep becomes significant. The onset of room temperature creep appears to coincide approximately with the outer surface hoop stress reaching 0.72 SMYS. This confirms that limiting the permissible stress to 0.72 SMYS would be sensible if one wishes to avoid creep. In all cases the rate of change of strain decayed rapidly with time and stabilised at a value of strain up to 15% higher than that initially recorded after a period of about five minutes.
Table 5 compares the burst pressures obtained by different methods. The FE analysis successfully predicted the remote strain at burst to within 2.7% of the actual burst pressure. This confirms the accuracy of the FE analysis and also the accuracy of the failure criterion from Fu and Kirkwood (1995a), which is also the basis for the guidance given in BS7910. The failure pressure calculated according to BS7910:1999 Annex G was 661bar, this is also very close to the actual burst pressure in the vessel of 662bar. The guidance given in BS7910 has been extensively validated against small-scale testing, full-scale testing and finite element analysis (Fu and Kirkwood 1995a, Batte et all 1997). It is therefore no coincidence that the two predicted burst pressures are similar and correspond so well with the actual experimentally determined burst pressure. The predicted burst pressure was 2.7% higher than the actual burst pressure, this discrepancy could be because the stress-strain curve in the FE-Analysis was based on an average of the three measured curves. If the FE-Analysis prediction was used for design purposes a lower bound stress-strain curve should be used.
Table 5 Comparison of the burst pressure obtained by different methods
FE-Analysis,
(bars) | BS7910:1999,
(bars) | Experimental,
(bars) |
|---|
| 680 |
661 |
662 |
Comparison of the measured and predicted axial and hoop strains away from the pit shows that the FE analysis was fairly accurate for these locations (see Fig.8). However, the FE analysis was less accurate at the pit location (see Fig.7). The accuracy of the predicted strain at the pit location may have been affected by the assumptions made in the FE modelling or inaccuracy in the strain gauge readings. However, the accuracy with which the FE analyses predicted the actual burst pressure indicates that the overall modelling procedure is satisfactory.
Examination of the section through the pit ( Fig.9) confirmed that failure took place by net section yielding.
Conclusions
Burst pressure has been accurately predicted using finite element analysis as well as assessment procedures given in BS7910:1999 Annex G for a corrosion pit representative of that found in a 8in production/test pipe, and the following conclusions can be drawn:
- Finite element analysis has shown that an 8in pipe with representative isolated pits of spherical diameter 25mm and 15mm are capable of surviving pressures in excess of 500 bar with remaining ligament thickness of 0.5mm without bursting.
- The comparison of burst pressure predictions with experimental results was also satisfactory, which gives added confidence in the modelling technique and the BS7910 Annex G procedure, for future applications.
References
Smith, A.T 'A critical review and comparison of various methods to evaluate the static strength of corroded pressurised components', Core research program TWI report (May 2000).
BS710:1999, 'Guide on methods for assessing the acceptability of flaws in metallic structures'. British Standard, London (1999).
ABAQUS version 5.6, Hibbitt, Karlsson and Sorenson Inc., 1080 Main Street, Pawtucket, Rhode Island, 1998.
Fu, B and Kirkwood, M. G. 1995a, 'Predicting failure pressure of internally corroded linepipe using the finite element method'. 1995 OMAE, Vol. V, Pipeline Technology, ASME 1995.
Fu, B and Kirkwood, M.G. 1995b, 'Determination of failure pressure of corroded linepipes using the non-linear finite element method'. In: R. Dennis ed. Pipeline Technology. Proc. 2 nd International pipeline technology conference, Ostend, Belgium, 11-14 Sept. 1995. Amsterdam: Elsevier. Vol 2. 1-10. ISBN 0444 82197X.
Batte, A.D., Fu, B., Kirkwood, M.G and Vu, D. 1997 'New method for determining the remaining strength of corroded pipelines'. In C. Guedes-Soares, et al, eds. 16 th Offshore Mechanics and Arctic Engineering Conference, Yokohama, Japan, 13-17 April 1997. New York: ASME Vol.5, pp 221-228.