Weld Joint Stress Intensity and Residual Stress Profiles

A Stacey (Health and Safety Executive, London, UK)

ASME-PVP
ASME Pressure Vessel and Piping Conference Symposium on Weld Residual Stresses and Fracture 23-27 July 2000

Abstract

Improved methods for including residual stresses in defect assessment procedures are becoming available. The latest generation of guidance documents, including BS 7910, API 579 and reports from the European SINTAP project, provide standard residual stress distributions for common welded joint configurations. Some also give stress intensity factor solutions for the non-linear distributions which are characteristic of residual stresses. In this paper, a standard distribution of residual stresses is referred to as a 'residual stress profile' or RSP, and K _RSP is the stress intensity factor at a defect subject to a RSP.

The new procedures for obtaining the RSP and K _RSP provide a practical alternative to the traditional assumption that 'residual stresses at welds are equal to yield'. The excessive conservatism which may be associated with that assumption can be reduced or eliminated. However, these new capabilities bring with them the danger of a 'black-box' syndrome. There are many different RSPs for different joint geometries and defect orientations, and the associated stress intensity factor solutions are complex. The fracture analyst may not be aware of the nature of the assumed residual stress distribution, or of the sensitivity of the assessment to the assumed residual stresses.

Examples are given in this paper of the variation of K _RSP as a function of crack size for a range of defect and weld configurations including long and short surface defects at butt and T-butt welds in plates and circumferential butt welds in cylinders. In order to demonstrate the benefits of using the standard residual stress profiles, the K _RSP values are compared with the stress intensity factor for the same defect subject to uniform yield magnitude residual stresses. A new solution is given for the K _RSP at a through-wall transverse crack subject to residual stresses having the trapezoidal shape given in the SINTAP and API 579 compendia for profiles of surface residual stresses.

Introduction

An interesting new development in residual stress technology is the compilation of standardised residual stress profiles (RSPs) for common types of welded joints. Within the last year, three new compendia of RSPs have been published. These may be found in Appendix Q of British Standard BS 7910:1999 ^[1] , in the final report ^[2] from Task 4 of the European collaborative project SINTAP, and in Appendix E of the draft API 579 ^[3] . Stress intensity factor solutions for the non-linear distributions which are characteristic of RSPs in welded joints are given in Appendix C of API 579 ^[3] and in a report ^[4] from Task 2 of the SINTAP project.

This paper starts with a summary and comparison of the RSPs in the three documents listed above ^[1-3] . Examples are given of stress intensity factors for a range of common defect and weld combinations, mostly calculated using the profiles and stress intensity solutions given in reports ^[2,4] from the SINTAP project. These examples illustrate the variation of stress intensity with crack depth, and the benefits to be obtained by assuming a non-linear RSP, as opposed to the traditional assumption of uniform residual stresses equal to the yield strength. Further examples are given in another SINTAP report ^[5] .

Comparison of published residual stress profiles

Table 1 summarises the RSPs available in BS 7910 ^[1] Appendix Q, the SINTAP compendium ^[2] and API 579 ^[3] Appendix E, categorised by joint type. The first compendium of RSPs known to the present authors was compiled by Mathieson ^[6] in 1991 for use in conjunction with the R6 assessment procedure. Very limited guidance on RSPs was given in BS PD 6493:1991 ^[7] (now superseded by BS 7910:1999 ^[1] ). Bate, Green and Buttle ^[8] reviewed the source data and RSPs in References 6 and 7 , and considered additional data with particular reference to offshore construction. They provided recommendations for revisions to the R6 compendium ^[6] . The current British ^[1] and European ^[2] compendia are based on further review and refinement of References 6 to 8 , and many of the RSPs are common to both documents and are similar or identical to profiles given in the earlier documents. The profiles in API 579 ^[3] Appendix E have some similarities with the BS 7910 ^[1] and the SINTAP compendia ^[2] : many have similar shapes; like SINTAP, API 579 gives four profiles for each joint type, namely the through-wall and surface profiles of longitudinal and transverse stresses (BS 7910 gives only through-wall profiles); and many of the same source references are quoted. However, the equations of the profiles in API 579 are entirely different from those in References 1 and 2 : it is evident that they are based on an independent review of the source data.

Table 1. Comparison of residual stress profiles in BS 7910, SINTAP and API 579

	BS 7910 [1] Appendix Q	SINTAP Compendium of RS Profiles [2]	API 579 [3] Appendix E
Materials	Ferritic steels, austenitic steels	Ferritic steels, austenitic steels, aluminium.	'Currently, a distinction is not made concerning the material of construction'
Distributions	Through-wall profiles	Through-wall and surface profiles.	Through-wall and surface profiles.
Straight full penetration butt welds	Q.1.2 Plate butt welds Q.1.4 Pipe axial seam welds (same as Q.1.2)	Fig.1 Plate butt welds and pipe axial seam welds	E4 Welds in piping and pressure vessel cylindrical shells. Single-V (E4.3) and double-V (E.4.4) longitudinal welds E6 Welds in storage tanks. Single-V (E.6.3) and double-V (E.6.4) longitudinal welds
Curved full penetration butt welds	Q.1.3 Pipe circumferential butt welds	Fig.3 Pipe butt welds	E4 Welds in piping and pressure vessel cylindrical shells. Single-V (E4.1) and double-V (E4.2) circumferential welds. E5 Welds in spheres and pressure vessel heads Single-V (E5.1) and double-V (E5.2) circumferential welds. Single-V (E5.3) and double-V (E5.4) meridional welds E6 Welds in storage tanks. Single-V (E6.1) and double-V (E6.2) circumferential welds
T-butt and T-fillet welds	Q.1.5 T-butt and fillet welds. Stresses in main plate at toe of weld at plate-to-plate, tube-to-plate and tube-to-tube joints. Two alternative profiles are given.	Fig.2 Plate T-butt welds (whose heat input is known) Appendix 3 Plate T-butt welds (where heat input is not known) Fig.4 Pipe T-butt welds	E8 Full penetration and fillet welds at a tee joint E8.1 Main plate E8.2 Stay plate
Nozzle attachment welds		Fig.5 Set-in nozzle Fig.6 Set-on nozzle	E7 Full penetration welds at corner joints (nozzles or piping branch connections) E7.1 Corner joint E7.2 Nozzle fillet weld E7.3 Shell fillet weld at a reinforcing pad
Repair welds	Q.1.6 Repair welds.	Fig.7 Repair welds	E9 Repair welds E9.1 Seam welds E9.2 Nozzle welds

BS 7910 and the SINTAP compendium are intended to be generally applicable for the assessment of flaws in welded structures. API 579 is concerned specifically with pressurised equipment used in the refinery and chemical industry. This difference of scope has led to some differences in the categorisation of weld types, as shown in Table 1. It should be noted that different terminologies are used for describing directions in API 579 compared with the other source documents, as summarised in Table 2. At circumferential welds, the term longitudinal refers to the cylinder axial direction in API 579, and to the circumferential direction (along the weld) in the other documents.

Table 2. Terminology for directions

	This paper/BS 7910/SINTAP	API 579
Direction of stress relative to weld	Longitudinal	Parallel
	Transverse	Perpendicular
Direction of welding in cylinders	Circumferential	Circumferential
	Axial	Longitudinal

Within the general categories of straight and curved full penetration butt welds in Table 1, BS 7910 and SINTAP give one set of RSPs for butt welds in flat plates and pipe axial seam welds, and one set of RSPs for circumferential butt welds in pipes. API 579 does not consider butt welds in flat plates, but gives separate sets of RSPs for welds in (i) piping and pressure vessel cylindrical shells, (ii) storage tanks and (iii) spheres and pressure vessel heads. It gives separate RSPs for longitudinal, circumferential and meridional welds, and for single-V and double-V welds.

 

For T-butt and T-fillet welds, BS 7910 and SINTAP give separate consideration to welds in plated construction and tubular construction. API 579 does not make this distinction, but does give profiles of stresses in the main plate and the stay plate.

With regard to the actual shapes of the profiles, the through-wall RSPs in BS 7910 and SINTAP include linear, bilinear, polynominal (up to 6 ^th order) and cosine profiles. Those in API 579 are more consistent in shape, all being linear, bilinear or 2 ^nd or 3 ^rd order polynominals. The surface RSPs in SINTAP and API 579 are trapezoidal, i.e. uniform inside the weld and decreasing linearly to zero in parent plate adjacent to the weld.

All the RSPs in API 579 and about half of those in BS 7910 and SINTAP are based on upperbound curves fitted to published residual stress data obtained by measurement or numerical modelling. The remainder of the RSPs in BS 7910 and SINTAP, including the surface profiles of longitudinal stresses and the bilinear through-wall profiles at the toes of T-butt and T-fillet welds, are based on a theoretical upper bound model of the extent of the plastically deformed zone adjacent to a weld developed by Leggatt ^[9,10] . The dimensions of the deformed zone are given as a function of material properties, weld heat input and plate thickness. The theoretically based profiles have been compared with relevant experimental and numerical solutions in the SINTAP project ^[2] , and found to be satisfactory. The theoretical model assumes a high restraint against thermal contraction after welding, which is an appropriate assumption for longitudinal stresses in nearly all cases, and for transverse stresses at T-joints in thicker materials (i.e. thicker than about 25mm). However, it may be less realistic in thinner materials, such that the RSPs become increasingly conservative as thickness decreases.

The empirically-based RSPs are strictly valid only within the range of plate thickness and welding conditions for which data were available. They have been non-dimensionalised with respect to plate thickness or weld width. This does not reflect the influence of welding and other parameters included in the theoretical model on the width of the plastically deformed zones adjacent to the welds. Hence the empirically-based RSPs may be over-conservative for thicknesses greater than those for which source data was available, and may be non-conservative for thicknesses below the range of the source data.

Longitudinal surface cracks at straight butt weld

Longitudinal cracks are subject to transverse residual stresses. Through-wall RSPs for transverse residual stresses at butt welds are shown in Fig.1. The residual stress is normalised with respect to the yield strength, and the depth from the surface, z, is normalised with respect to the wall thickness, t. BS 7910 ^[1] and SINTAP ^[2] give the same profile, which is a 6 ^th order polynominal and is applicable for plate butt welds and axial seam welds. API 579 gives a 2 ^nd order polynominal (Eq.E.34) for single-V longitudinal welds and uniform stresses (Eq.E.43) for double-V longitudinal welds in piping and cylindrical pressure vessels, and a linear profile (Eq.E.73) for single-V welds and a 2 ^nd order polynominal (Eq.E.79) for double-V welds in storage tanks.

API 579 Eq.E.34 and E.79 are somewhat similar to the BS 7910 and SINTAP profiles, except in the region 0.4<z/t<0.9 where the API profiles are more tensile. API 579 Eq.E43 adopts the traditional conservative assumption of uniform yield magnitude stresses at double-V longitudinal welds in pipes and cylindrical pressure vessels, but Eq.E73 shows stresses decreasing linearly to zero at the root of single-V welds in storage tanks. The present authors would not be confident of always finding zero stress or less at this location: tensile transverse stresses can develop at the root of the weld as it is stretched by angular distortion during the deposition of the fill passes.

The 'normalised K _RSP', i.e. the stress intensity factor corresponding to the standard residual stresses profile divided by Equation.1. , is plotted versus normalised crack depth for infinite longitudinal surface cracks at straight butt welds in Fig.2. The K _RSP was calculated using a weight function solution given as Equation AI.3 in the SINTAP stress intensity factor handbook ^[4] . The normalised K _RSP for the BS 7910 and SINTAP profiles is approximately equal to 1.0 for crack depths 0<a/t<0.4, but then starts to rise, despite the presence of compressive stresses in this region. The normalised K _RSP for uniform yield stress Equation.2. (as in API 579 Eq.E.43) starts at 1.0, but rises faster than the K _RSP for a non-linear profile, as would be expected. This demonstrates the benefit to be obtained by using the non-linear RSP, where this is deemed to be applicable. K _RSP has not been calculated for the linear profile defined by API 579 Eq.E.73, but this may be expected to lie between the solutions shown in Fig.2.

All the K _RSP values discussed above apply to long surface cracks at the side welded last (BS 7910), or at the outside (API 579). For cracks at the opposite face, the normalised K _RSP would tend to zero as the crack depth tends to zero for the RSP defined by API Eq.E.73 and to about 1.0 for the other profiles shown in Fig.1. This is clearly a significant difference, and further work to confirm the validity of Eq.E.73 in this region would be desirable.

 

The normalised K _RSP for the deepest and surface intersection points of semi-elliptical surface cracks of aspect ratio, 2c/a, equal to 3.33 and 10 are plotted in Fig.3. K _RSP was evaluated using a solution for a 5 ^th order polynominal stress profile ^[4] , and hence it was necessary to fit a 5 ^th order polynominal to the 6 ^th order BS 7910/SINTAP profile shown in Fig.1.

In contrast to the K _RSP shown in Fig.2 for infinite surface cracks, the normalised K _RSP shown in Fig.3 for the deepest point of finite surface cracks falls continuously with crack depth. The stress intensity factor is always positive, despite the presence of compressive stresses in the range 0.5<z/t<0.8. The normalised K _RSP at the surface intersection points of finite surface cracks is approximately constant at about 0.8 for an aspect ratio of 2c/a = 3.33, and is initially lower but rises with crack depth for a crack of aspect ratio 2c/a = 10. The stress intensity at the surface intersection point is greater than that at the deepest point for a/t > 0.1 with 2c/a = 3.33, and for a/t > 0.5 with 2c/a = 10.

 

Transverse through-wall cracks at butt weld

Transverse cracks at welds are subject to longitudinal residual stresses. The characteristic trapezoidal profile of longitudinal surface residual stresses recommended in BS 7910, SINTAP and API 579 is illustrated in Fig.4. For the purpose of assessing through-wall cracks, the usual practice is to assume that the given cross-weld profile of surface stresses is applicable throughout the thickness of the joint. The issue of interest is how the stress intensity factor changes as the crack length increases beyond the width of the tensile zone.

A solution for a through-wall crack in an infinite flat plate subject to a trapezoidal RSP was given in Ref 5 and is reproduced here. The solution was obtained by integrating the weight function solution given on page 5.11a of Ref 11 for a symmetrical point load, p, at a distance, y, from the centre of a crack length, 2a, in an infinite plate. For a transverse crack subjected to longitudinal stresses, Equation.3. the point load, p, is equated with the force Equation.4. acting on an infinitesimal length, dy, of the crack. Then Equation.5:

The solution for the trapezoidal profile shown in Fig.4 is as follows:

For

For

For

The normalised K _RSP for through-wall cracks subject to trapezoidal profiles with different widths of tensile zone from W ₂/W ₁ = 3 to 9 are shown in Fig.5. For a/W ₁ ≤ 0.5, the crack is within the weld, and is subject to yield magnitude stresses, giving normalised K _RSP=1. For a/W ₁>0.5, the crack length is greater than the weld width, and the normalised K _RSP falls with crack length, at a rate dependent on the total width of the tensile zone. The use of the trapezoidal RSP removes the conservatism inherent in the traditional assumption of residual stresses equal to yield strength for cracks whose width is greater than the weld width.

Longitudinal surface cracks at T-joints

Figure 6 shows the through-wall profiles of transverse residual stresses in the main plate at the toes of T-butt or T-fillet welds. The BS 7910 Eq.Q.13 and SINTAP Fig.4d RSP is a 4 th order polynominal with one peak just below the toe and a second peak near the back surface. The other profiles fall from yield stress at the toe to zero at an internal location. For the bilinear profiles given by BS 7910 Eq.Q.9 and SINTAP Fig.2d, the depth of the tensile zone, z o, is a function of the heat input of the weld pass adjacent to the weld toe and the material properties. These profiles are applicable where z o ≤t. If the validity of the bilinear RSP is accepted, then, for crack depths up to a/t = 0.5, the curved profiles of API 579 E.94, BS 7910 Eq.Q.13 and SINTAP Fig.4d would seem to be over-conservative for z o/t = 0.25, approximately correct for z o/t = 0.5, and unconservative (at greater crack depths) for z o/t = 0.75.

Normalised K _RSP values for longitudinal surface cracks of aspect ratio 2c/a = 3.33, 10 and infinity at the toe of a T-butt weld are shown in Fig.7. These were evaluated assuming the bilinear profile shown in Fig.6 with z _o/t = 0.5. They were evaluated using a solution from the SINTAP stress intensity factor handbook ^[4] for a semi-elliptical surface crack in a plate subject to through-wall stress profile expressed as a 5 ^th order polynominal. Hence it was necessary to fit a 5 ^th order polynominal to the bilinear profile, which gave a very good fit. It can be seen that the normalised K _RSP rises with crack depth for an infinitely long surface crack, but falls for cracks of finite length.

The normalised K _RSP for the deepest and surface intersection points of longitudinal surface cracks of aspect ratio 2c/a = 3.33 at the toes of T-butt welds subject to uniform residual stress, Img.5. or the bilinear profile with z _o/t = 0.5 are shown in Fig.8. The K _RSP values for the bilinear profiles were calculated for the region 0>a/t>0.5, where the profile is linear, and hence could be expressed in terms of a membrane and bending component. All K _RSP values in Fig.8 were calculated using the well-known solutions by Newman and Raju ^[12] . The normalised K _RSP values rise with crack depth under uniform yield stresses. They fall with crack depth at the deepest point of a crack subject to the bilinear RSP, but remain approximately constant with crack depth at the surface intersection point, which is the controlling location for crack depths, a/t>0.15. Hence, the benefit of using the bilinear profile is smaller than would be expected on the basis of the stress intensity at the deepest point of the crack.

Circumferential surface cracks at circumferential butt welds

This type of crack is subject to the through-wall profile of transverse residual stresses (i.e. parallel to the cylinder axis) at circumferential butt welds. Published RSPs for these welds are shown in Fig.9. The SINTAP compendium ^[2] , Fig.3d, gives different profiles for values of heat input per unit thickness, q/vt, higher or lower than 60J/mm ². The SINTAP low heat input profile is shown for q/vt = 60J/mm ² : the profile is scaled down at lower values of q/vt, with a limiting scaling factor of 0.5 as q/vt tends to very low value. The SINTAP high heat profile has a cosine distribution and is not subject to scaling. The API 579 'low thickness' profile is applicable for t* ≤20mm when q/v ≤2kJ/mm, and for t* ≤50mm where q/v>2kJ/mm. The API 579 'high thickness' profile is applicable for t* ≥70mm when q/v ≤2kJ/mm, and for t* ≥100mm when q/v>2kJ/mm. t* is a modified thickness parameter dependent on R/t, and is equal to the thickness t for R/t ≤10. The RSP is scaled between the low and high thickness lines at intermediate values of t*.

Drawings in API 579 and the SINTAP compendium imply that the single sided weld is made from the outside : the profiles would be different if the weld was made from the inside.

API 579 has, in general, adopted a more conservative approach than SINTAP, in as much as the former gives entirely tensile stresses while the latter gives compressive stresses at various locations. The two approaches show some agreement with respect to the stresses at the root of the weld (i.e. at z/t=1). Both methods agree that the stress is a function of heat input, q/v, and thickness, t. API gives yield tensile stresses for low thickness conditions, and SINTAP gives yield tensile stresses for high heat input per unit thickness (i.e. for low thickness). Both methods give reduced tensile stresses at the root for high thickness or low q/vt conditions.

Although the two profiles given by SINTAP have undoubtedly been observed in practice, it is difficult to reconcile the abrupt change in profile at the transitional value of q/vt=60J/mm ². It is also the case that some observations have been made of zero or low tensile stresses at the outside face, z/t=0. Hence, the API profiles may be considered more appropriate for surface defects located at the outside surface. On the other hand, the tensile peak shown in the SINTAP high heat input RSP at z/t=0.4 has also been observed in practice, and the API 579 profiles may be unconservative for buried defects at this location.

Normalised K _RSP values corresponding to the SINTAP high heat and low heat profiles and to uniform yield stresses acting on a full circumferential defect at the root of a circumferential butt weld are shown in Fig.10. These were calculated using a weight function solution. The normalised K _RSP for uniform yield residual stresses rises gradually from 1.2 at a/t=0 to 2.0 at a/t=0.6. The normalised K _RSP for the SINTAP high heat RSP falls gradually with crack depth from 1.2 at a/t=0, and hence would provide some benefit in terms of reduced K _RSP at crack depths a/t>0.2. The normalised K _RSP for API low thickness RSP (not shown) would lie between the uniform yield stress and SINTAP high heat curves and hence would be of limited benefit.

The normalised K _RSP for the SINTAP low heat RSP falls rapidly with crack depth, and hence would show significant benefit, even for shallow cracks. The normalised K _RSP for the API 579 high thickness RSP (not shown) can be obtained by scaling down the uniform yield stress solution by 0.2, and hence would also show considerable benefit compared with the assumption of uniform yield stresses.

 

Summary and conclusions

• Three sets of standardised residual stress profiles for common weld joint types have recently become available.
• Many of the profiles given in BS 7910:1999 ^[1] Appendix Q and the SINTAP project residual stress compendium ^[2] are identical: those in API 579 ^[3] Appendix E show some similarities with the BS 7910 and SINTAP profiles, but have different equations.
• Areas where one or other of the published profiles may be unconservative or over-conservative have been discussed in this paper.
• A SINTAP project report ^[4] and API 579 ^[3] provide stress intensity factor solutions applicable to non-linear residual stress profiles.
• The reduction in stress intensity factor obtained by using the published profiles instead of the traditional assumption of uniform yield magnitude residual stresses has been quantified for a range of examples.
• A new solution for the stress intensity factor at a through-wall crack subject to a trapezoidal residual stress profile is presented.
• Further investigation of the transverse residual stresses at circumferential butt welds is needed.

Nomenclature

a	half-length of through crack or depth of surface crack
c	half-length of finite surface crack
K 1	stress intensity factor
K RSP	stress intensity factor at crack subject to RSP
q	weld power
R	radius
RS	residual stress
RSP	residual stress profile
t	thickness
t*	modified thickness
v	weld travel speed
W 1	width of weld
W 2	total width of tensile zone
y	transverse direction
z	through-wall direction
z o	depth of tensile zone
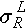	longitudinal residual stress
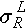	transverse residual stress
σ Y	yield strength
σ YP	parent metal yield strength
σ YW	weld metal yield strength

Acknowledgments

This paper was based in part on work done at TWI under sub-contract to the Health and Safety Executive, as part of SINTAP, a collaborative project supported by the European Commission. The authors acknowledge the support of their project partners and sponsors.

References

1	BS 7910:1999:	'Guidance on methods for assessing the acceptability of flaws in fusion welded structures'. British Standards Institution, April 1999.
2	Barthelemy J Y:	'SINTAP Task 4. Compendium of residual stress profiles'. Final Report. Institut de Soudure, May 1999.
3	API:	'Recommended practice for fitness-for-service'. Issue 12, September 1999 (Special Release).
4	Al Laham S:	'SINTAP Task 2.6. Stress intensity factor and limit load handbook'. British Energy Generation Ltd, EPD/GEN/REP/0316/98, Issue 2, April 1998.
5	Leggatt R H and Sanderson R M:	'Stress intensity due to residual stresses TWI report SINTAP/TWI/4-6 88269/46/99, September 1999.
6	Mathiesen P A R:	'A compendium of as-welded residual stress profiles'. Nuclear Electric memorandum TD/SIB/MEM/0233, September 1991.
7	BSI:	'Guidance on methods for assessing the acceptability of flaws in fusion welded structures'. BSI Published Document PD 6493:1991.
8	Bate S K, Green D and Buttle D J:	'A review of residual stress distributions in welded joints for the defect assessment of offshore structures'. Offshore Technology Report OTH 95-482. London, The Stationery Office, September 1995.
9	Leggatt R H:	'Welding residual stresses'. In: The 5 th International Conference on Residual Stresses (ICRS5), Linköping, Sweden, 16-18 June, 1997. Eds Ericsson T, Oden M, Andersson A, Linköping University, Sweden. Vol.1.pp12-25.
10	Leggatt R H:	'Recommendations for revised surface residual stress profiles'. TWI report SINTAP/TWI/4-3 88269/4-3/98, June 1998.
11	Tada H, Paris P and Irwin G:	'The stress analysis of cracks handbook'. Del Research Corporation, Second Edition, 1985.
12	Newman J C and Raju I S:	'Stress-intensity factor equations for cracks in three-dimensional finite bodies subjected to tension and bending loads'. NASA Technical Memorandum 85793, April 1984.