Ferritic steel fracture toughness based on Charpy energy

Direct measurement of fracture toughness is preferable, but there are several Charpy/fracture toughness correlations which can be used where this is not possible. Three correlations are given in Annex J of BS 7910, 2013 ('Guide to methods for assessing the acceptability of flaws in metallic structures'). Two of these are used for materials on the lower shelf/transition of the ductile/brittle transition curve, whilst the third is recommended for upper shelf behaviour.

1) For steels on the lower shelf and in the transition region, a simple lower bound estimate of toughness can be made from the Charpy energy at the same temperature ^[1] as follows:

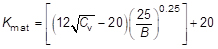
where:

Kmat	is the estimate of the fracture toughness (in MPa √m);
B	is the thickness of the material for which an estimate of Kmat is required (in mm);
Cv	is the lower bound Charpy V-notch impact energy at the service temperature (in Joules)

2) The so-called Master Curve approach^[2] can be used to make a preliminary estimate of the fracture toughness of ferritic steels from Charpy energy. This is a well-validated approach which is based on a correlation between the 27J or 40J Charpy transition temperature and the temperature at which a 25mm thick fracture mechanics specimen shows a fracture toughness, K_mat, of 100MPa √m. Although the approach has been extensively validated for a range of parent steels, there are cases where it overestimates K_mat, especially the following cases:

• where Charpy specimens exhibit unusual behaviour such as fracture path deviation; this may occur in hard, narrow welds made by laser or electron beam welding
• where splits are present on the fracture surface of fracture toughness specimens
• where microstructure and properties vary through the section thickness, making it difficult to ensure that the Charpy specimen samples the same microstructure as that associated with initiation in the fracture toughness specimen
• where material is heavily cold-worked

It is thus highly advisable for users to assure themselves that the correlation is applicable to any particular case.

The method takes into account the test temperature, (T), 27J or 40J transition temperature (T_27J or T_40J), the 100MPa√m transition temperature (T₀), the thickness of the specimen (B), and desired probability of failure (P_f).

T₀ is derived from the Charpy transition temperature as follows:

T₀ = T_27J -18 °C    [2]
T₀ = T_40J -24 °C     [3]

where:

T₀ is the temperature for median toughness of 100MPa √m in 25mm thick specimens; T_27J and T_40J are the temperature for energies of 27J and 40J, respectively, measured in a standard 10 x 10mm Charpy V specimen.

Toughness at a given temperature is then given by the equation:

where:

Kmat	is in MPa√m;
T	is the temperature at which Kmat is to be determined (in °C);
T0	is estimated from equations [2] and [3];
TK	is the temperature term that describes the scatter in the Charpy versus fracture toughness correlation given by equations [2] and [3]. For a standard deviation of 15°C and 90% confidence, T K =+25°C;
B	is the thickness of the material for which an estimate of Kmat is required (in mm);
Pf	is the probability of Kmat being less than estimated. The use of P f = 0.05 (5%) is recommended unless experimental evidence supports the use of a higher probability for a given material.

units: K_mat in MPa√m, T, T₀, T_k, T_27J, T_40J in °C, B in mm. A value P_f =0.05 (5%) is recommended for initial assessments.

Note that equation [4] increases without limit as the temperature is increased, and it is important to take into account the onset of upper shelf behaviour, so that the upper shelf toughness is not overestimated (see equation[5]).

K_mat = 0.54 C_v + 55    [5]

where:

Kmat	is the estimated fracture toughness (in MPa √m);
Cv	is the lower bound Charpy V-notch impact energy at the service temperature for which Kmat is required (in Joules).

 

API579-1/ASME FFS-1 recommends an alternative approach to fracture toughness estimation, based on the ASME reference curve, but based on Charpy testing alone, i.e. without the use of Pellini tests.

References

1. INSTA Technical Report, 1991: 'Assessment of structures containing discontinuities', Materials Standards Institution, Stockholm.
2. Wallin, K: 'Simple theoretical Charpy V-K_Ic correlation for irradiation embrittlement', in Innovative approaches to irradiation damage and fracture analysis, ed DL Marriott, TR Mayer, WH Barnford, New York: ASME. PVP-170. 93.100. ISBN 0791803260