Die Finite-Elemente-Analyse (FEA) ist ein Verfahren, bei dem das Verhalten eines Bauteils oder einer Baugruppe unter gegebenen Bedingungen simuliert wird, so dass es mit der Finite-Elemente-Methode (FEM) bewertet werden kann. Ingenieure verwenden die Finite-Elemente-Analyse, um physikalische Phänomene zu simulieren und dadurch den Bedarf an Prototypen zu reduzieren und gleichzeitig die Optimierung von Komponenten als Teil des Konstruktionsprozesses eines Projekts zu ermöglichen.
Die FEA verwendet mathematische Modelle, um die Auswirkungen von realen Bedingungen auf ein Teil oder eine Baugruppe zu verstehen und zu quantifizieren. Diese Simulationen, die mit Hilfe spezieller Software durchgeführt werden, ermöglichen es den Ingenieuren, potentielle Probleme in einem Entwurf zu lokalisieren, einschließlich Spannungsspitzen und Schwachstellen.
Mit Hilfe der Mathematik ist es möglich, das Struktur- oder das Strömungsverhalten, die Wellenausbreitung, den Wärmetransport und andere Phänomene zu verstehen und zu quantifizieren.
Die meisten Prozesse können mit Hilfe partieller Differentialgleichungen beschrieben werden, aber diese komplexen Gleichungen müssen gelöst werden, damit Parameter wie Spannung und Dehnungsraten abgeschätzt werden können. Die FEA ermöglicht eine näherungsweise Lösung dieser Probleme.
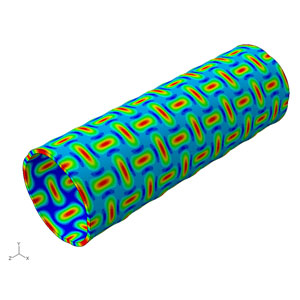
Die Finite-Elemente-Analyse ist die Grundlage moderner Software-Simulationssoftware, wobei die Ergebnisse in der Regel mit einer computergenerierten Farbskala dargestellt werden.
Wo liegen die Ursprünge der FEA?
Während einige Theorien besagen, dass die FEA ihre Wurzeln in den Arbeiten von Euler aus dem 16. Jahrhundert hat, gehen die frühesten mathematischen Arbeiten, die die Technik direkt beschreiben, auf Schellbachs Arbeit von 1851 zurück. Die FEA wurde von Ingenieuren aus verschiedenen Industriezweigen weltweit weiterentwickelt, um eine große Anzahl strukturmechanischer Probleme, vor allem im Bauwesen und in der Luft- und Raumfahrt, zu lösen. Die erste Entwicklung von FEA für reale Anwendungen begann Mitte der 1950er Jahre und wurde in den nächsten Jahrzehnten weiterentwickelt.
Wie funktioniert die Finite-Elemente-Analyse?
Die in der FEA verwendeten Simulationen werden mit Hilfe eines Netzes aus Millionen kleinerer Elemente erstellt, die zusammen die Form der zu bewertenden Struktur bilden. Jedes dieser kleinen Elemente wird Berechnungen unterzogen, wobei diese Netzverfeinerungen zusammen das Endergebnis der gesamten Struktur ergeben.
Diese Näherungsberechnungen sind in der Regel polynomisch, wobei Interpolationen über die kleinen Elemente erfolgen, was bedeutet, dass an einigen, aber nicht an allen Punkten Werte bestimmt werden können. Die Punkte, an denen die Werte bestimmt werden können, werden als Knotenpunkte bezeichnet und befinden sich normalerweise an der Grenze des Elements.
Was ist die Finite-Elemente-Methode?
Die Finite-Elemente-Methode (FEM) ist ein bei unterschiedlichen physikalischen Aufgabenstellungen angewendetes numerisches Verfahren, das auf der numerischen Lösung eines komplexen Systems aus Differentialgleichungen basiert. Damit kann eine Festigkeits- und Verformungsuntersuchung von Festkörpern mit geometrisch komplexer Form durchgeführt werden, wenn der Einsatz von klassischen Methoden (z. B. die Balkentheorie) zu aufwendig oder nicht möglich wäre.
Partielle Differentialgleichungen
Wie oben erwähnt, kann die Finite-Elemente-Analyse zur näherungsweisen Lösung partieller Differentialgleichungen verwendet werden, aber gelegentlich ist es besser, die Differentialgleichungen konventionell zu lösen.